题目内容
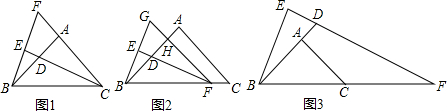
如图，△ABC中，AD是角平分线，DE∥AC交AB于E，已知AB=12，AC=8，求DE．考点：相似三角形的判定与性质
专题：
分析：如图，首先证明EA=ED（设为λ）；然后证明△BDE∽△BCA，列出比例式
=
，即
=
，求出λ即可解决问题．
| DE |
| AC |
| BE |
| AB |
| λ |
| 8 |
| 12-λ |
| 12 |
解答：解：如图，∵AD是角平分线，DE∥AC，
∴∠EDA=∠DAC，∠EAD=∠DAC，
∴∠EDA=∠EAD，EA=ED（设为λ）；
则BE=12-λ；
∵DE∥AC，
∴△BDE∽△BCA，
∴
=
，即
=
，
解得：λ=
，
即DE的长为
．
解：如图，∵AD是角平分线，DE∥AC，∴∠EDA=∠DAC，∠EAD=∠DAC，
∴∠EDA=∠EAD，EA=ED（设为λ）；
则BE=12-λ；
∵DE∥AC，
∴△BDE∽△BCA，
∴
| DE |
| AC |
| BE |
| AB |
| λ |
| 8 |
| 12-λ |
| 12 |
解得：λ=
| 24 |
| 5 |
即DE的长为
| 24 |
| 5 |
点评：该题主要考查了角平分线的定义、相似三角形的判定及其性质等几何知识点及其应用问题；应深入观察图形，数形结合，准确找出图形中隐含的等量关系．
练习册系列答案
相关题目
下列计算中正确的是（ ）
| A、（-x）9÷（-x）3=x6 |
| B、a3•a2=a6 |
| C、a8÷a2=a4 |
| D、x3+x3=x6 |
对于反比例函数y=
，下列说法正确的是（ ）
| 1 |
| x |
| A、图象经过点（1，-1） |
| B、图象是中心对称图形 |
| C、图象位于第二、四象限 |
| D、当x＜0时，y随x的增大而增大 |
