题目内容
如图1,一次函数y=2x+4与x轴,y轴分别相交于A,B两点,一次函数图象与坐标轴围成的△ABO,我们称它为此一次函数的坐标三角形.把坐标三角形面积分成相等的二部分的直线叫做坐标三角形的等积线.
(1)求此一次函数的坐标三角形周长以及分别过点A、B的等积线的函数表达式;
(2)如图2,我们把第一个坐标三角形△ABO记为第一代坐标三角形.第一代坐标三角形的等积线BA1,AB1记为第一对等积线,它们交于点O1,四边形A1OB1O1称为第一个坐标四边形.求点O1的坐标和坐标四边形A1OB1O1面积;
(3)如图3.第一对等积线与坐标轴构成了第二代坐标三角形△BA1O.△AOB1分别过点A,B作一条平分△BA1O,△AOB1面积的第二对等积线BA2,AB2,相交于点O2,如此进行下去.…,请直接写出On的坐标和第n个坐标四边形面积(用n表示).

(1)求此一次函数的坐标三角形周长以及分别过点A、B的等积线的函数表达式;
(2)如图2,我们把第一个坐标三角形△ABO记为第一代坐标三角形.第一代坐标三角形的等积线BA1,AB1记为第一对等积线,它们交于点O1,四边形A1OB1O1称为第一个坐标四边形.求点O1的坐标和坐标四边形A1OB1O1面积;
(3)如图3.第一对等积线与坐标轴构成了第二代坐标三角形△BA1O.△AOB1分别过点A,B作一条平分△BA1O,△AOB1面积的第二对等积线BA2,AB2,相交于点O2,如此进行下去.…,请直接写出On的坐标和第n个坐标四边形面积(用n表示).

考点:一次函数综合题
专题:压轴题
分析:(1)令y=0求出x的值,令x=0求出x的值,从而得到点A、B的坐标,再求出OA、OB的长,然后利用勾股定理列式求出AB,再根据三角形的周长公式列式计算即可得解;根据等积线的定义求出A1、B1的坐标,然后利用待定系数法求一次函数解析式解答;
(2)联立两等积线解析式求解即可得到O1的坐标,再根据坐标四边形A1OB1O1面积=S△AOB1-S△AA1O1,列式计算即可得解;
(3)根据等积线的定义求出OAn、OBn,从而得到An、Bn的坐标,再利用待定系数法写出ABn、BAn的解析式,联立求解即可得到点On的坐标,再根据坐标四边形面积=S△AOBn-S△AAnOn,列式计算即可得解.
(2)联立两等积线解析式求解即可得到O1的坐标,再根据坐标四边形A1OB1O1面积=S△AOB1-S△AA1O1,列式计算即可得解;
(3)根据等积线的定义求出OAn、OBn,从而得到An、Bn的坐标,再利用待定系数法写出ABn、BAn的解析式,联立求解即可得到点On的坐标,再根据坐标四边形面积=S△AOBn-S△AAnOn,列式计算即可得解.
解答:解:(1)令y=0,则2x+4=0,
解得,x=-2,
令x=0,则y=4,
∴点A(-2,0),B(0,4),
∴OA=2,OB=4,
由勾股定理得,AB=
=
=2
,
所以,周长为6+2
,
∵AB1、BA1是等积线,
∴A1(-1,0),B1(0,2),
∴等积线的函数表达式:y=4x+4,y=x+2;
(2)联立
,
解得
,
∴O1(-
,
),
坐标四边形A1OB1O1面积=S△AOB1-S△AA1O1,
=
×2×2-
×(2-1)×
,
=2-
,
=
;
(3)由题意得,OAn=
,OBn=
,
所以,等积线BAn的解析式为:y=2n+1x+4,
ABn的解析式为:y=
x+
,
联立
解得
,
∴点On(-
,
),
坐标四边形面积=S△AOBn-S△AAnOn,
=
×2×
-
×(2-
)×
,
=
-
,
=
,
=
.
解得,x=-2,
令x=0,则y=4,
∴点A(-2,0),B(0,4),
∴OA=2,OB=4,
由勾股定理得,AB=
| OA2+OB2 |
| 22+42 |
| 5 |
所以,周长为6+2
| 5 |
∵AB1、BA1是等积线,
∴A1(-1,0),B1(0,2),
∴等积线的函数表达式:y=4x+4,y=x+2;
(2)联立
|
解得
|
∴O1(-
| 2 |
| 3 |
| 4 |
| 3 |
坐标四边形A1OB1O1面积=S△AOB1-S△AA1O1,
=
| 1 |
| 2 |
| 1 |
| 2 |
| 4 |
| 3 |
=2-
| 2 |
| 3 |
=
| 4 |
| 3 |
(3)由题意得,OAn=
| 2 |
| 2n |
| 4 |
| 2n |
所以,等积线BAn的解析式为:y=2n+1x+4,
ABn的解析式为:y=
| 1 |
| 2n+1 |
| 4 |
| 2n |
联立
|
|
∴点On(-
| 2 |
| 2n+1 |
| 4 |
| 2n+1 |
坐标四边形面积=S△AOBn-S△AAnOn,
=
| 1 |
| 2 |
| 4 |
| 2n |
| 1 |
| 2 |
| 2 |
| 2n |
| 4 |
| 2n+1 |
=
| 4 |
| 2n |
| 4(2n-1) |
| 2n(2n+1) |
=
| 8 |
| 2n(2n+1) |
=
| 23-n |
| 2n+1 |
点评:本题是一次函数综合题型,主要利用了一次函数与坐标轴的交点坐标的求解,联立两函数解析式求交点坐标,读懂题目信息,理解等积线是三角形的相应的中线是解题的关键.

练习册系列答案
相关题目
 在正方形网格中,△ABC的位置如图所示,则cosA的值为( )
在正方形网格中,△ABC的位置如图所示,则cosA的值为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,在四边形ABCD中,AB∥CD,∠A=∠C,四边形ABCD是平行四边形吗?为什么?
如图,在四边形ABCD中,AB∥CD,∠A=∠C,四边形ABCD是平行四边形吗?为什么? 在平面直角坐标系xOy中,抛物线y=x2+bx+c与x轴交于A、B两点(点A在点B的左侧),点B的坐标为(3,0),与y轴交于点C(0,3),顶点为D.
在平面直角坐标系xOy中,抛物线y=x2+bx+c与x轴交于A、B两点(点A在点B的左侧),点B的坐标为(3,0),与y轴交于点C(0,3),顶点为D. 一小贩设计一个转盘游戏(如图),2元玩一次,玩家旋转转盘,当转盘停止时,指针指向的物品即为玩家所获物品,若指针指向分界线,则重玩一次.小贩这样设计有道理吗?为什么?
一小贩设计一个转盘游戏(如图),2元玩一次,玩家旋转转盘,当转盘停止时,指针指向的物品即为玩家所获物品,若指针指向分界线,则重玩一次.小贩这样设计有道理吗?为什么?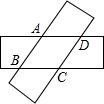 如图,用两张等宽的矩形纸片叠合在一起,记重叠部分为四边形ABCD,你认为它是什么特殊的四边形?请动手叠一叠,并说明你的理由.
如图,用两张等宽的矩形纸片叠合在一起,记重叠部分为四边形ABCD,你认为它是什么特殊的四边形?请动手叠一叠,并说明你的理由.