题目内容
9．在Rt△ABC中，∠ACB=90°，AB=4，AC=2，则cosB=$\frac{\sqrt{3}}{2}$．分析 先画出图形，根据余弦的定义，可得答案．
解答 解：如图所示：
BC=$\sqrt{{AB}^{2}-A{C}^{2}}$=2$\sqrt{3}$，
cosB=$\frac{BC}{AB}$=$\frac{{\sqrt{3}}}{2}$．
故答案为：$\frac{\sqrt{3}}{2}$．
点评 本题考查了锐角三角函数的定义，解答本题的关键是求出BC的长度，另外此题也可直接用特殊角的三角函数值求解．
练习册系列答案
相关题目
19．
如图，△ABE和△CDE是以点E为位似中心的位似图形，点E的坐标为（1，0），若点A、C、D的坐标分别是（3，4）、（2，2）、（3，1）．则点D的对应点B的坐标是（ ）
如图，△ABE和△CDE是以点E为位似中心的位似图形，点E的坐标为（1，0），若点A、C、D的坐标分别是（3，4）、（2，2）、（3，1）．则点D的对应点B的坐标是（ ）| A． | （4，2） | B． | （4，1） | C． | （5，2） | D． | （5，1） |
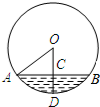一条排水管的截面如图所示，已知该排水管的半径OA=10，水面宽AB=16，则排水管内水的最大深度CD=4．
14．下列图形不是轴对称图形的有（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
一个矩形苗圃，一边靠墙，另外三边用长为30米的篱笆围成，墙长为14米，设这个苗圃园垂直于墙的一边的长为x米．求：