题目内容
2. 超速行驶是引发交通事故的主要原因.上周末,小明和三位同学尝试用自己所学的知识检测车速,如图,观测点设在到县城城南大道的距离为100米的点P处.这时,一辆出租车由西向东匀速行驶,测得此车从A处行驶到B处所用的时间为4秒,且∠APO=60°,∠BPO=45°.
超速行驶是引发交通事故的主要原因.上周末,小明和三位同学尝试用自己所学的知识检测车速,如图,观测点设在到县城城南大道的距离为100米的点P处.这时,一辆出租车由西向东匀速行驶,测得此车从A处行驶到B处所用的时间为4秒,且∠APO=60°,∠BPO=45°.(1)求A、B之间的路程;
(2)请判断此出租车是否超过了城南大道每小时60千米的限制速度?
分析 (1)利用三角函数在两个直角三角形中分别计算出BO、AO的长,即可算出AB的长;
(2)利用路程÷时间=速度,计算出出租车的速度,再把60千米/时化为$\frac{50}{3}$米/秒,再进行比较即可.
解答 解:(1)由题意知:PO=100米,∠APO=60°,∠BPO=45°,
在直角三角形BPO中,
∵∠BPO=45°,
∴BO=PO=100米,
在直角三角形APO中,
∵∠APO=60°,
∴AO=PB•tan60°=100$\sqrt{3}$米,
∴AB=AO-BO=(100$\sqrt{3}$-100)=100($\sqrt{3}$-1)(米);
(2)∵从A处行驶到B处所用的时间为4秒,
∴速度为100($\sqrt{3}$-1)÷4=25($\sqrt{3}$-1)米/秒,
∵60千米/时=$\frac{60×1000}{3600}$=$\frac{50}{3}$米/秒,
而25($\sqrt{3}$-1)>$\frac{50}{3}$,
∴此车超过了每小时60千米的限制速度
点评 此题是解直角三角形的应用,主要考查了锐角三角函数,从复杂的实际问题中整理出直角三角形并求解是解决此类题目的关键.

练习册系列答案
相关题目
12.计算(-1)2016+(-1)2018所得的结果为( )
| A. | 0 | B. | 1 | C. | -1 | D. | 2 |
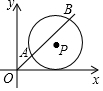 如图,在平面直角坐标系中,点P的坐标为(a,5),半径为5的⊙P交直线y=x于点A,B,若弦AB=8,-则a的值为5+3$\sqrt{2}$.
如图,在平面直角坐标系中,点P的坐标为(a,5),半径为5的⊙P交直线y=x于点A,B,若弦AB=8,-则a的值为5+3$\sqrt{2}$.