��Ŀ����
��ƽ��ֱ������ϵ�У���֪һ�κ���y=2x+1��ͼ��P1��x1��y1����P2��x2��y2�����㣬��x1��x2����y1 ______ y2�����������������=����
���𰸡���
�������������������һ�κ���y=2x+1��k=2��0��
��y��x�����������
��x1��x2��
��y1��y2��
���㣺һ�κ���ͼ���ϵ������������
�����͡������
��������
13
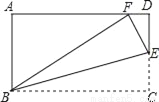
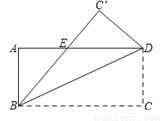
��ͼ���ھ���ABCD�У�AB=3��BC=5����CD����ȡһ��E������BE������BCE��BE�۵���ʹ��Cǡ������AD���ϵĵ�F������CE�ij�Ϊ_____��
��ϰ��ϵ�д�
�����Ŀ


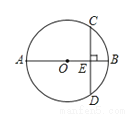
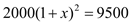
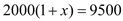
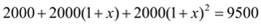
 DE��AB=
DE��AB=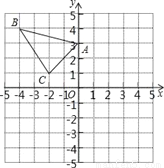
 B.
B.  C.
C. 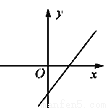 D.
D. 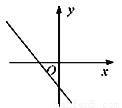
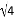 ��
��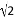 ��3.14��
��3.14�� 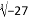 ��
�� ����6����������������( )
����6�����У�����������( )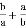 ��ֵ�ǣ� ��
��ֵ�ǣ� ��