题目内容
14.某乡镇的4个村庄A、B、C、D恰好位于正方形的4个顶点上,为了解决农民出行难问题,镇政府决定修建连接各村庄的道路系统,使得每两个村庄都有直达的公路,设计人员给出了如下四个设计方案(实线表示连接的道路)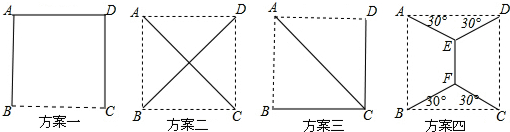
在上述四个方案中最短的道路系统是方案( )
| A. | 一 | B. | 二 | C. | 三 | D. | 四 |
分析 设正方形的边长为a,计算出各种情况时正方形的面积,然后进行比较从而解得.
解答 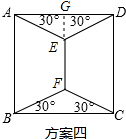 解:设正方形边长为a,则方案①需用线3a,方案②需用线2$\sqrt{2}$a,方案③需用线2a+$\sqrt{2}$a,
解:设正方形边长为a,则方案①需用线3a,方案②需用线2$\sqrt{2}$a,方案③需用线2a+$\sqrt{2}$a,
如图所示:
∵AD=a,
∴AG=$\frac{a}{2}$,AE=$\frac{\sqrt{3}}{3}$a,GE=$\frac{\sqrt{3}}{6}$a,
∴EF=a-2GE=a-$\frac{\sqrt{3}}{3}$a,
∴方案④需用线$\frac{\sqrt{3}}{3}$a×4+(a-$\frac{\sqrt{3}}{6}$a×2)=($\sqrt{3}$+1)a.
∴方案④最省钱.
故选D.
点评 本题考查的是作图-应用与设计作图,涉及到正方形的性质,设其正方形边长,分别计算出各自的面积,进行比较而得.

练习册系列答案
相关题目
9.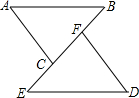 如图,△ABC与△DEF是全等三角形,即△ABC≌△DEF,那么图中相等的线段有( )
如图,△ABC与△DEF是全等三角形,即△ABC≌△DEF,那么图中相等的线段有( )
 如图,△ABC与△DEF是全等三角形,即△ABC≌△DEF,那么图中相等的线段有( )
如图,△ABC与△DEF是全等三角形,即△ABC≌△DEF,那么图中相等的线段有( )| A. | 1组 | B. | 2组 | C. | 3组 | D. | 4组 |
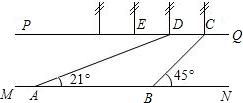 峨眉河是峨眉的一个风景点.如图,河的两岸PQ平行于MN,河岸PQ上有一排间隔为50米的彩灯柱C、D、E、…,小华在河岸MN的A处测得∠DAN=21°,然后沿河岸走了175米到达B处,测得∠CBN=45°,求这条河的宽度(参考数据:sin21°≈$\frac{9}{25}$,tan21°≈$\frac{3}{8}$).
峨眉河是峨眉的一个风景点.如图,河的两岸PQ平行于MN,河岸PQ上有一排间隔为50米的彩灯柱C、D、E、…,小华在河岸MN的A处测得∠DAN=21°,然后沿河岸走了175米到达B处,测得∠CBN=45°,求这条河的宽度(参考数据:sin21°≈$\frac{9}{25}$,tan21°≈$\frac{3}{8}$).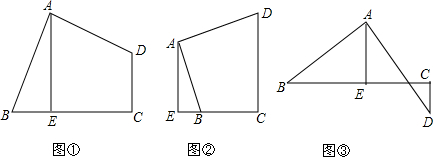
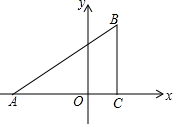 已知,如图,在平面直角坐标系中,△ABC是直角三角形,∠ACB=90°,点A,C的坐标分别为A(-3,0),C(1,0),BC=3.
已知,如图,在平面直角坐标系中,△ABC是直角三角形,∠ACB=90°,点A,C的坐标分别为A(-3,0),C(1,0),BC=3.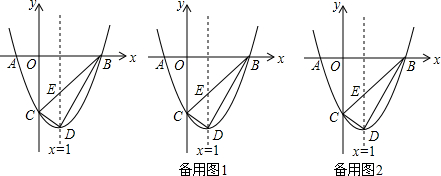
 如图,在平行四边形中挖去一个矩形,在请用无刻度的直尺,准确作出一条直线,将剩下图形的面积平分.(保留作图痕迹)
如图,在平行四边形中挖去一个矩形,在请用无刻度的直尺,准确作出一条直线,将剩下图形的面积平分.(保留作图痕迹)