题目内容
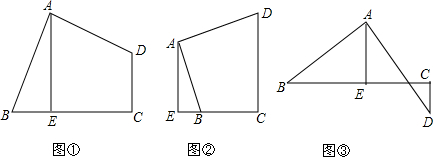
2.已知AB=AD,∠BAD=∠C=90°,AE⊥BC于E,(1)如图①,求证:BE+CD=AE;
(2)如图②图③,请直接写出BE、CD、AE之间的数量关系,不需要证明;
(3)若CE=8,BE=$\frac{1}{2}$AE,则CD=4或12.
分析 (1)过点D作DF⊥AE,垂足为F,证明△ABE≌△ADF,四边形CDFE为长方形,得BE=AF,CD=EF,即可得出BE+CD=AE;
(2)如图②过点A作AF⊥CD,垂足为F,证明△ABE≌△ADF,四边形AECF为长方形,得BE=DF,CF=AE,即可得出BE+AE=CD;如图③过点D作DF⊥AE,垂足为F,证明△ABE≌△ADF,四边形CDFE为长方形,得BE=AF,CD=EF,即可得出BE=CD+AE;
(3)根据(1)可得出DF=8,则AE=8,BE=4,得出CD=4,再(2)得AE=8,BE=4,得出CD=12;从而得出CD的长为4或12.
解答 解:(1)过点D作DF⊥AE,垂足为F,
∵AE⊥BC,
∴∠AEB=∠AEC=90°,
∴∠BAD=∠C=90°,
∴∠BAE=∠ADF,
在△ABE和△ADF中,
$\left\{\begin{array}{l}{∠BEA=∠AFD}\\{∠BAE=∠ADF}\\{AB=AD}\end{array}\right.$,
∴△ABE≌△ADF,
∴BE=AF,
∴四边形CDFE为长方形,
∴CD=EF,
∴BE+CD=AE;
(2)如图②;BE+AE=CD;
如图③;BE=CD+AE;
(3)如图①,得BE+CD=AE;
∵DF=CE=8,
∴AE=8,
∴BE=4,
∴CD=4,
如图②,得BE+AE=CD;
∵AF=CE=8,
∴AE=8,
∴BE=4,
∴CD=12;
∴CD的长为4或12.
故答案为4或12.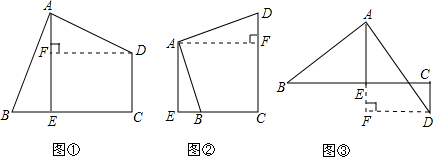
点评 本题考查了全等三角形的判定和性质,解题的关键是构造全等三角形,证明线段相等,注意转化思想的运用,难度不大,是中考常见题型.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
7.下列事件是随机事件的是( )
| A. | 在一个标准大气压下,加热到100℃,水沸腾 | |
| B. | 购买一张福利彩票,中奖 | |
| C. | -2的绝对值小于0 | |
| D. | 在一个仅装着白球和黑球的袋中摸球,摸出红球 |
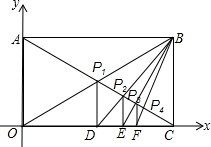 平面直角坐标系中,矩形OABC的顶点A,C分别在坐标轴上,顶点B在第一象限内,如图所示,且OA=a,OC=b.请根据下列操作,完成后面的问题.
平面直角坐标系中,矩形OABC的顶点A,C分别在坐标轴上,顶点B在第一象限内,如图所示,且OA=a,OC=b.请根据下列操作,完成后面的问题.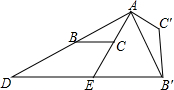 如图,△ABC中,AC=2,把△ABC绕点A逆时针旋转90°得到△AB′C′,过点B′作BC的平行线,分别交AB、AC的延长线于D、E两点,∠AED=120°,EB′=2$\sqrt{3}$,AB的长为2$\sqrt{3}$.
如图,△ABC中,AC=2,把△ABC绕点A逆时针旋转90°得到△AB′C′,过点B′作BC的平行线,分别交AB、AC的延长线于D、E两点,∠AED=120°,EB′=2$\sqrt{3}$,AB的长为2$\sqrt{3}$.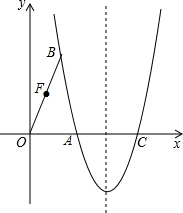 如图,在平面直角坐标系中,抛物线y=$\frac{8\sqrt{2}}{5}$x2+bx+c经过点A($\frac{3}{2}$,0)和点B(1,2$\sqrt{2}$),与x轴的另一个交点为C.
如图,在平面直角坐标系中,抛物线y=$\frac{8\sqrt{2}}{5}$x2+bx+c经过点A($\frac{3}{2}$,0)和点B(1,2$\sqrt{2}$),与x轴的另一个交点为C.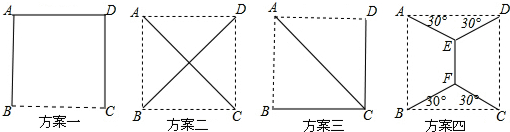
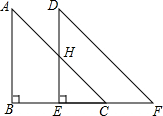 如图,将直角△ABC沿BC边平移得到直角△DEF,AB=6cm,BE=3cm,DH=3cm,求四边形CHDF的面积为多少cm2?
如图,将直角△ABC沿BC边平移得到直角△DEF,AB=6cm,BE=3cm,DH=3cm,求四边形CHDF的面积为多少cm2?