Question

11．一游泳池有进水闸，放水闸各1个，单独进水4h可以装满一池水，单独放水6h可以放完一池水，当池中的水占满池的$\frac{1}{4}$时，同时打开进水闸和放水闸．设两闸开放的时间用xh表示，池中的水占满池的几分之几用y表示．
（1）求y与x之间的函数表达式，并写出自变量x的取值范围；
（2）在平面直角坐标系中画出题（1）中的函数图象；
（3）求泳池从有$\frac{1}{4}$池水到有$\frac{1}{2}$池水时两闸开放的时间．

Answer 1

分析 （1）根据工作总量与工作效率和工作时间的关系列出函数解析式即可；
（2）根据一次函数的解析式画出图象即可；
（3）把y=$\frac{1}{2}$代入解析式解答即可．

解答 解：（1）y与x之间的函数表达式为：y=$\frac{1}{4}x-\frac{1}{6}x+\frac{1}{4}=\frac{1}{12}x+\frac{1}{4}$，
由$\left\{\begin{array}{l}{x≥0}\\{\frac{1}{4}x-\frac{1}{6}x≤1-\frac{1}{4}}\end{array}\right.$，
解得：0≤x≤9，
所以自变量的取值范围是：0≤x≤9；
（2）图象如图：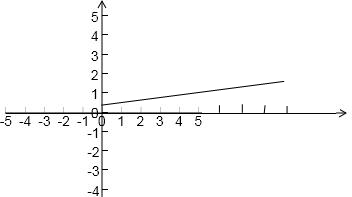
（3）把y=$\frac{1}{2}$代入解析式可得：$\frac{1}{2}=\frac{1}{12}x+\frac{1}{4}$，
解得：x=3，
答：两闸开放的时间是3小时．

点评 此题考查一次函数的应用，关键是根据工作总量与工作效率和工作时间的关系列出函数解析式．