题目内容
14.阅读下列材料:关于x的方程x2-3x+1=0(x≠0)方程两边同时乘以$\frac{1}{x}$得:x-3+$\frac{1}{x}$=0即x+$\frac{1}{x}$=3
(x+$\frac{1}{x}$)2=x2+$\frac{1}{{x}^{2}}$+2•x•$\frac{1}{x}$=x2+$\frac{1}{{x}^{2}}$+2
x2+$\frac{1}{{x}^{2}}$=(x+$\frac{1}{x}$)2-2=32-2=7
根据以上材料,解答下列问题:
(1)x2-4x+1=0(x≠0),则x2+$\frac{1}{{x}^{2}}$=14,x4+$\frac{1}{{x}^{4}}$=194
(2)2x2-7x+2=0(x≠0),求x3+$\frac{1}{{x}^{3}}$的值.
分析 (1)根据例题方程两边同时除以x,即可求得x+$\frac{1}{x}$的值,然后平方即可求得x2+$\frac{1}{{x}^{2}}$的值,然后再平方求得x4+$\frac{1}{{x}^{4}}$的值;
(2)首先方程两边除以2x即可求得x+$\frac{1}{x}$的值,然后平方即可求得x2+$\frac{1}{{x}^{2}}$的值,然后利用立方差公式求解.
解答 解:(1)方程两边同时乘以$\frac{1}{x}$得:x-4+$\frac{1}{x}$=0,则x+$\frac{1}{x}$=4,
两边平方得x2+$\frac{1}{{x}^{2}}$+2=16,则x2+$\frac{1}{{x}^{2}}$=14,
两边平方得x4+$\frac{1}{{x}^{4}}$+2=196,则x4+$\frac{1}{{x}^{4}}$=194.
故答案是:14,194;
(2)方程两边同时除以2x得x-$\frac{7}{2}$+$\frac{1}{x}$=0,
则x+$\frac{1}{x}$=$\frac{7}{2}$,
两边平方得x2+$\frac{1}{{x}^{2}}$+2=$\frac{49}{4}$,则x2+$\frac{1}{{x}^{2}}$=$\frac{41}{4}$,
x3+$\frac{1}{{x}^{3}}$=(x+$\frac{1}{x}$)(x2+$\frac{1}{{x}^{2}}$-1)=$\frac{7}{2}$×($\frac{41}{4}$-1)=$\frac{7}{2}$×$\frac{37}{4}$=$\frac{259}{8}$.
点评 本题考查平方差公式以及立方差公式,正确理解平方差公式的变形是关键.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
6. 如图,五角星围绕中心O旋转,旋转角至少为多少度才能与自身重合( )
如图,五角星围绕中心O旋转,旋转角至少为多少度才能与自身重合( )
 如图,五角星围绕中心O旋转,旋转角至少为多少度才能与自身重合( )
如图,五角星围绕中心O旋转,旋转角至少为多少度才能与自身重合( )| A. | 36° | B. | 72° | C. | 108° | D. | 144° |
4.下列判断中,正确的是( )
| A. | x的系数是0 | B. | y的次数是0 | ||
| C. | 23xyz是三次单项式 | D. | 24与42不是同类项 |
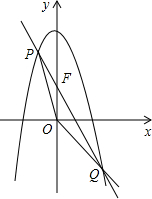 抛物线y=-x2+10,直线l过点F(0,4),交抛物线于P、Q两点,是否存在直线l,使S△POF:S△QOF=1:3?若存在,求直线l的解析式;若不存在,请说明理由.
抛物线y=-x2+10,直线l过点F(0,4),交抛物线于P、Q两点,是否存在直线l,使S△POF:S△QOF=1:3?若存在,求直线l的解析式;若不存在,请说明理由.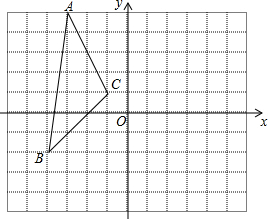 如图,直角坐标系中,A(-3,5),B(-4,-2),C(-1,1).
如图,直角坐标系中,A(-3,5),B(-4,-2),C(-1,1).