题目内容
5.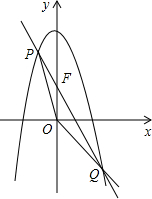 抛物线y=-x2+10,直线l过点F(0,4),交抛物线于P、Q两点,是否存在直线l,使S△POF:S△QOF=1:3?若存在,求直线l的解析式;若不存在,请说明理由.
抛物线y=-x2+10,直线l过点F(0,4),交抛物线于P、Q两点,是否存在直线l,使S△POF:S△QOF=1:3?若存在,求直线l的解析式;若不存在,请说明理由.
分析 根据直线l过F(0,4),设直线l的解析式为y=kx+4,根据题意设P(a,-a2+10),Q(-3a,-9a2+10),代入直线l的解析式y=kx+4,即可求得k的值,进而求得直线l的解析式.
解答 解:设P(a,-a2+10),
∵S△EOC:S△FOC=1:3,
∴Q(-3a,-9a2+10),
∵直线与y轴的交点坐标为(0,4),
∴设直线l的解析式为y=kx+4,
把P、Q代入得
$\left\{\begin{array}{l}{-{a}^{2}+10=ak+4}\\{-9{a}^{2}+10=-3ak+4}\end{array}\right.$,
解得k=±2$\sqrt{2}$,
∴直线l的解析式为y=2$\sqrt{2}$x+4或y=-2$\sqrt{2}$x+4.
点评 本题考查了二次函数的性质,待定系数法求一次函数的解析式,分析出P、Q两点的横坐标的特点是解题的关键.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
15.若x2=5,则(2x3)2÷(4x4)的值为( )
| A. | 10 | B. | $\frac{5}{2}$ | C. | 25 | D. | 5 |
16.若四边形两条对角线相等,则顺次连接其各边中点得到的四边形是( )
| A. | 菱形 | B. | 矩形 | C. | 梯形 | D. | 正方形 |
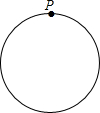 有一长为240米的圆形跑道,小明和他的小狗同时从跑道的点P处出发沿顺时针方向跑步,已知小明的速度为4米/秒,小狗的速度为12米/秒,跑步的时间记为t秒,在跑步过程中,小明和他的小狗之间相距(取两者之间较短一段圆弧跑道的长度)为w米
有一长为240米的圆形跑道,小明和他的小狗同时从跑道的点P处出发沿顺时针方向跑步,已知小明的速度为4米/秒,小狗的速度为12米/秒,跑步的时间记为t秒,在跑步过程中,小明和他的小狗之间相距(取两者之间较短一段圆弧跑道的长度)为w米