题目内容
10．若实数a，b，c满足a2+b2+c2=0，求代数式（a-b）2+（b-c）2+（c-a）2的最大值0．分析 根据完全平方公式得到（a-b）2+（b-c）2+（c-a）2=2a2+2b2+2c2-2ab-2ac-2bc，由（a-b）2≥0，即2ab≤a2+b2，于是有-2ab-2ac-2bc≥-（2a2+2b2+2c2），然后把a2+b2+c2=0代即可得到最大值．
解答 解：∵（a-b）2≥0，
∴2ab≤a2+b2，
∵a2+b2+c2=0，
∴（a-b）2+（b-c）2+（c-a）2
=2a2+2b2+2c2-2ab-2ac-2bc
∴-2ab-2ac-2bc≥-（2a2+2b2+2c2）
∴2ab+2ac+2bc≤0．
∴代数式（a-b）2+（b-c）2+（c-a）2的最大值0．
故答案为：0．
点评 此题考查整式的化简求值，完全平方公式：（a±b）2=a2±2ab+b2．也考查了（a-b）2的非负性质以及代数式的变形能力．
练习册系列答案
相关题目
18．下列长度的3条线段，能构成三角形的是（ ）
| A． | 1cm，4cm，3cm | B． | 2cm，3cm，4cm | C． | 4cm，4cm，8cm | D． | 5cm，6cm，12cm |
5．下面计算正确的是（ ）
| A． | 3+$\sqrt{3}$=3$\sqrt{3}$ | B． | $\sqrt{12}$÷$\sqrt{3}$=2 | C． | $\sqrt{2}$•$\sqrt{3}$=$\sqrt{5}$ | D． | $\sqrt{（-6）^{2}}$=-6 |
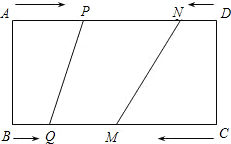如图所示，在长方形ABCD中，BC=24cm，AB=10cm，点P，Q，M，N分别从A，B，C，D出发沿AD，BC，CB，DA方向在长方形的边上同时运动，当有一个点先到达所在运动边的另一个端点时，运动即停止．已知在相同时间内，若BQ=xcm（x≠0），则AP=2xcm，CM=3xcm，DN=x2cm．
19．已知$\frac{a}{b}$=$\frac{3}{4}$，则$\frac{a+b}{b}$=（ ）
| A． | $\frac{1}{4}$ | B． | $\frac{3}{4}$ | C． | $\frac{7}{4}$ | D． | $\frac{4}{7}$ |