题目内容
17. 在平面直角坐标系中,反比例函数y=$\frac{m}{x}$(x>0,m是常数)的图象经过点A(1,4)、点B(a,b),其中a>1.过点A作x轴的垂线,垂足为C,过点B作y轴的垂线,垂足为D,AC与BD相交于点M,连接DC、AB.
在平面直角坐标系中,反比例函数y=$\frac{m}{x}$(x>0,m是常数)的图象经过点A(1,4)、点B(a,b),其中a>1.过点A作x轴的垂线,垂足为C,过点B作y轴的垂线,垂足为D,AC与BD相交于点M,连接DC、AB.(1)求反比例函数;
(2)求证:DC∥AB.
分析 (1)把A坐标代入反比例解析式求出m的值,即可确定出解析式;
(2)把B坐标代入反比例解析式表示出b,由A与B的坐标表示出C,D,M的坐标,进而表示出DM,MB,AM,MC的长,得出两边对应成比例,且夹角相等,确定出三角形CDM与三角形ABM相似,利用相似三角形对应角相等得到一对内错角相等,利用内错角相等两直线平行即可得证.
解答 (1)解:∵A(1,4)在函数y=$\frac{m}{x}$图象上,
∴把A坐标代入得:m=4,
则反比例解析式为y=$\frac{4}{x}$;
(2)证明:由题意得:B(a,$\frac{4}{a}$),C(1,0),D(0,$\frac{4}{a}$),M(1,$\frac{4}{a}$),
∴DM=1,MB=a-1,AM=4-$\frac{4}{a}$,MC=$\frac{4}{a}$,
∵$\frac{DM}{MC}$=$\frac{a}{4}$,$\frac{MB}{AM}$=$\frac{a-1}{4-\frac{4}{a}}$=$\frac{a}{4}$,
∴$\frac{DM}{MC}$=$\frac{MB}{AM}$,
∵∠DMC=∠BMA,
∴△CDM∽△ABM,
∴∠DCA=∠BAC,
∴DC∥AB.
点评 此题属于反比例函数综合题,涉及的知识有:待定系数法确定反比例函数解析式,坐标与图形性质,相似三角形的判定与性质,以及平行线的判定,熟练掌握待定系数法是解本题第一问的关键.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案
相关题目
9.下列各式中,能用平方差公式计算的是( )
| A. | (3x+2y)(2x-3y) | B. | (2x+3)(3-2x) | C. | (2b-a)(a-2b) | D. | (m+2)(n-2) |
6.已知正比例函数y=(2m-1)x在图象上有两点A(x1、y1)、B(x2、y2),当x1<2时,y1<y2,则m的取值范围是( )
| A. | m$<\frac{1}{2}$ | B. | m$>\frac{1}{2}$ | C. | m<2 | D. | m>0 |
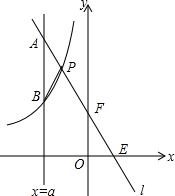 如图,一次函数y=k1x+b的图象l与坐标轴分别交于点E、F,与双曲线y=-$\frac{{k}_{2}}{x}$(x<0)交于点P(-1,4),且F是PE的中点.
如图,一次函数y=k1x+b的图象l与坐标轴分别交于点E、F,与双曲线y=-$\frac{{k}_{2}}{x}$(x<0)交于点P(-1,4),且F是PE的中点.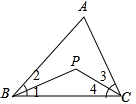 如图,BP、CP分别平分∠ABC和∠ACD
如图,BP、CP分别平分∠ABC和∠ACD 如图,在梯形ABCD中,AD∥BC,对角线AC⊥BD且AC=12,BD=5,则梯形的高DE=$\frac{60}{13}$.
如图,在梯形ABCD中,AD∥BC,对角线AC⊥BD且AC=12,BD=5,则梯形的高DE=$\frac{60}{13}$.