Question

6．如图1，已知△ABC中，∠BAC=90°，AB=AC，AE是过A的一条直线，且BD⊥AE于点D，CE⊥AE于点E．
（1）根据图1试证明：△ABD≌△CAE，并说明BD与DE，CE的关系：BD=DE=CE．
（2 ）若直线AE绕A点旋转到图2位置时（BD＞CE），其余条件不变，试说明BD与DE，CE的关系又如何？（需把证明过程写出来）

Answer 1

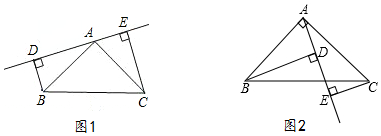
分析 （1）BD=DE-CE，根据已知利用AAS判定△ABD≌△CAE，从而得到BD=AE，AD=CE，因为AD+AE=BD+CE，所以BD=DE-CE；
（2）BD=DE+CE成立，根据已知利用AAS判定△ABD≌△CAE，从而得到BD=AE，AD=CE，因为AE=AD+DE，所以BD=DE+CE．

解答 解：（1）BD=DE-CE；
如图1，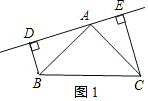

∵∠BAC=90°，BD⊥AE，CE⊥AE，
∴∠BDA=∠AEC=90°，
∴∠ABD+∠DAB=∠DEB+∠CAE，
∴∠ABD=∠CAE，
∵AB=AC，
在△ABD和△CAE中，
∵$\left\{\begin{array}{l}{∠BDA=∠AEC}\\{∠ABD=∠CAE}\\{AB=AC}\end{array}\right.$，
∴△ABD≌△CAE（AAS），
∴BD=AE，AD=CE，
∴AD+AE=BD+CE，
∵DE=BD+CE，
∴BD=DE-CE．

（2）BD=DE+CE，
如图2，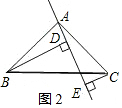

∵∠BAC=90°，BD⊥AE，CE⊥AE，
∴∠BDA=∠AEC=90°，
∵∠ABD+∠BAE=90°，∠CAE+∠BAE=90°
∴∠ABD=∠CAE，
∵AB=AC，
在△ABD和△CAE中，
∵$\left\{\begin{array}{l}{∠BDA=∠AEC}\\{∠ABD=∠CAE}\\{AB=AC}\end{array}\right.$，
∴△ABD≌△CAE（AAS），
∴BD=AE，AD=CE，
∵AE=AD+DE，
∴BD=DE+CE．

点评 本题主要考查学生对全等三角形的判定方法的理解及运用，熟练掌握全等三角形的判定与性质是解题的关键，常用的判定方法有SSS，SAS，AAS．