题目内容
18.某车库出口处设置有“两段式栏杆”,点A是栏杆转动的支点,点E是栏杆两段的连接点,当车辆经过时,栏杆AEF升起后的位置如图1所示(图2为其几何图形).其中AB⊥BC,DC⊥BC,EF∥BC,∠EAB=150°,AB=AE=1.2m,BC=2.4m.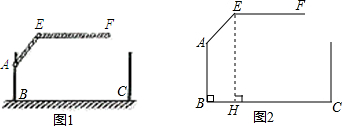
(1)求图2中点E到地面的高度(即EH的长.$\sqrt{3}$≈1.73,结果精确到0.01m,栏杆宽度忽略不计);
(2)若一辆厢式货车的宽度和高度均为2m,这辆车能否驶入该车库?请说明理由.
分析 (1)利用锐角三角函数关系得出EM的长进而得出EH的长;
(2)利用已知得出△EPK∽△EAM,进而得出PK的长,再求出PR的长进而得出答案.
解答 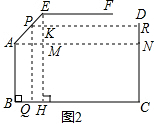 解:(1)如图,作AM⊥EH于点M,交CD于点N,
解:(1)如图,作AM⊥EH于点M,交CD于点N,
则四边形ABHM和MHCN都是矩形,
∵∠EAB=150°,∴∠EAM=60°,
又∵AB=AE=1.2米,
∴EM=0.6$\sqrt{3}$≈0.6×1.73=1.038≈1.04(米),
∴EH≈2.24(米);
(2)如图,在AE上取一点P,过点P分别作BC,CD的垂线,垂足分别是Q,R,PR交EH于点K,不妨设PQ=2米,
下面计算PR是否小于2米;
由上述条件可得EK=EH-PQ=0.24米,AM=0.6米,
∵PK∥AM,∴△EPK∽△EAM,
∴$\frac{PK}{AM}$=$\frac{EK}{EM}$,即$\frac{PK}{0.6}$=$\frac{0.24}{0.6\sqrt{3}}$,
∴PK=0.08$\sqrt{3}$(米),
∴PR=PK+MN=PK+BC-AM=0.08$\sqrt{3}$+2.4-0.6
=1.8+0.08$\sqrt{3}$
≈1.94(米),
∵PR<2米,∴这辆车不能驶入该车库.
点评 此题主要考查了相似三角形的应用以及锐角三角函数关系,熟练应用相似三角形的性质是解题关键.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
9.下列图形中,既不是轴对称图形,又不是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
3.已知点A(-2,1),B(1,4),若反比例函数y=$\frac{k}{x}$与线段AB有公共点时,k的取值范围是( )
| A. | -$\frac{9}{4}$≤k<0或0<k≤4 | B. | k≤-2或k≥4 | C. | -2≤k<0或k≥4 | D. | -2≤k<0或0<k≤4 |
10.某运动品牌专卖店准备购进甲、乙两种运动鞋.其中甲、乙两种运动鞋的进价和售价如下表.已知购进60双甲种运动鞋与50双乙种运动鞋共用10000元
(1)求m的值;
(2)要使购进的甲、乙两种运动鞋共200双的总利润(利润=售价-进价)超过21000元,且不超过22000元,问该专卖店有几种进货方案?
(3)在(2)的条件下,专卖店准备决定对甲种运动鞋每双优惠a(50<a<70)元出售,乙种运动鞋价格不变.那么该专卖店要获得最大利润应如何进货?
| 运动鞋价格 | 甲 | 乙 |
| 进价(元/双) | m | m-20 |
| 售价(元/双) | 240 | 160 |
(2)要使购进的甲、乙两种运动鞋共200双的总利润(利润=售价-进价)超过21000元,且不超过22000元,问该专卖店有几种进货方案?
(3)在(2)的条件下,专卖店准备决定对甲种运动鞋每双优惠a(50<a<70)元出售,乙种运动鞋价格不变.那么该专卖店要获得最大利润应如何进货?
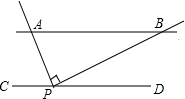 如图,AB∥CD,点P在CD上,且AP⊥BP,∠ABP=25°,则∠APC=65度.
如图,AB∥CD,点P在CD上,且AP⊥BP,∠ABP=25°,则∠APC=65度.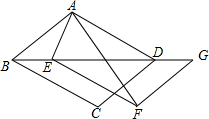 如图,在平行四边形ABCD中,∠ABD=30°,AB=4,BD=5$\sqrt{3}$,将△BCD沿方向平移BD,得到△EFG.
如图,在平行四边形ABCD中,∠ABD=30°,AB=4,BD=5$\sqrt{3}$,将△BCD沿方向平移BD,得到△EFG.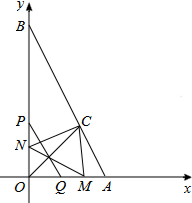 如图,已知点A(2,0),B(0,4),∠AOB的角平分线交AB于C,一动点P从O点出发,以每秒2个单位长度的速度,沿y轴向点B作匀速运动,过点P且平行于AB的直线交x轴于Q,作P,Q关于直线OC的对称点M,N.设P运动的时间为t(0<t<2)秒
如图,已知点A(2,0),B(0,4),∠AOB的角平分线交AB于C,一动点P从O点出发,以每秒2个单位长度的速度,沿y轴向点B作匀速运动,过点P且平行于AB的直线交x轴于Q,作P,Q关于直线OC的对称点M,N.设P运动的时间为t(0<t<2)秒