题目内容
10.某运动品牌专卖店准备购进甲、乙两种运动鞋.其中甲、乙两种运动鞋的进价和售价如下表.已知购进60双甲种运动鞋与50双乙种运动鞋共用10000元| 运动鞋价格 | 甲 | 乙 |
| 进价(元/双) | m | m-20 |
| 售价(元/双) | 240 | 160 |
(2)要使购进的甲、乙两种运动鞋共200双的总利润(利润=售价-进价)超过21000元,且不超过22000元,问该专卖店有几种进货方案?
(3)在(2)的条件下,专卖店准备决定对甲种运动鞋每双优惠a(50<a<70)元出售,乙种运动鞋价格不变.那么该专卖店要获得最大利润应如何进货?
分析 (1)根据“购进60双甲种运动鞋与50双乙种运动鞋共用10000元”列出方程并解答;
(2)设购进甲种运动鞋x双,表示出乙种运动鞋(200-x)双,然后根据总利润列出一元一次不等式,求出不等式组的解集后,再根据鞋的双数是正整数解答;
(3)设总利润为W,根据总利润等于两种鞋的利润之和列式整理,然后根据一次函数的增减性分情况讨论求解即可.
解答 解:(1)依题意得:60m+50(m-20)=10000,
解得m=100;
(2)设购进甲种运动鞋x双,则乙种运动鞋(200-x)双,
根据题意得,$\left\{\begin{array}{l}{(240-100)x+(160-80)(200-x)>21000①\\}\\{(240-100)x+(160-80)(200-x)≤22000②}\end{array}\right.$,
解不等式①得,x>$\frac{250}{3}$,
解不等式②得,x≤100,
所以,不等式组的解集是$\frac{250}{3}$<x≤100,
∵x是正整数,100-84+1=17,
∴共有17种方案;
(3)设总利润为W,则W=(240-100-a)x+80(200-x)=(60-a)x+16000($\frac{250}{3}$<x≤100),
①当50<a<60时,60-a>0,W随x的增大而增大,
所以,当x=100时,W有最大值,
即此时应购进甲种运动鞋100双,购进乙种运动鞋100双;
②当a=60时,60-a=0,W=16000,(2)中所有方案获利都一样;
③当60<a<70时,60-a<0,W随x的增大而减小,
所以,当x=84时,W有最大值,
即此时应购进甲种运动鞋84双,购进乙种运动鞋116双.
点评 本题考查了一次函数的应用,分式方程的应用,一元一次不等式组的应用,解决问题的关键是读懂题意,找到关键描述语,进而找到所求的量的等量关系和不等关系,(3)要根据一次项系数的情况分情况讨论.


| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | 1 |
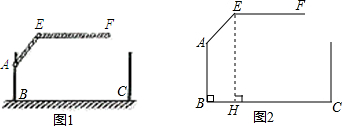
 将两个含30°和45°的直角三角板如图放置,则∠α的度数是( )
将两个含30°和45°的直角三角板如图放置,则∠α的度数是( )| A. | 10° | B. | 15° | C. | 20° | D. | 25° |
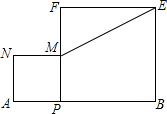 如图,线段AB=10,点P是AB的动点,分别以AP、BP为边在线段AB的同侧作正方形APMN、PBEF,连结ME,则ME的最小值是2$\sqrt{5}$.
如图,线段AB=10,点P是AB的动点,分别以AP、BP为边在线段AB的同侧作正方形APMN、PBEF,连结ME,则ME的最小值是2$\sqrt{5}$.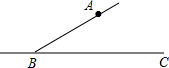 利用尺规作图(保留作图痕迹即可):如图,在射线BC上,作线段BD,使BD=2AB;以点D为顶点,射线DC为一边,作∠EDC(两种情况),使∠EDC=∠ABC.
利用尺规作图(保留作图痕迹即可):如图,在射线BC上,作线段BD,使BD=2AB;以点D为顶点,射线DC为一边,作∠EDC(两种情况),使∠EDC=∠ABC.