题目内容
如图，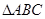
是等边三角形，CE是外角平分线，点D在AC上，连结BD并延长与CE交于点E.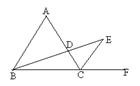
（1）直接写出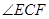
的度数等于__________°；
（2）求证：△ABD∽△CED；
（3）若AB=12，AD=2CD，求BE的长.
（1）
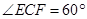；（2）根据等边三角形的性质可得
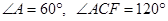，再由
平分
结合对顶角相等即可证得结论；（3）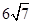
.
解析试题分析：（1）根据等边三角形及外角平分线的性质即可求得结果；
（2）根据等边三角形的性质可得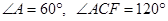 ，再由平分结合对顶角相等即可证得结论；
（3）作BG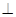
AC于G，根据等边三角形三线合一的性质可得
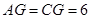，由
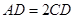可得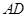
、CD的长，再根据勾股定理即可求得BG、BD的长，由（1）得△ABD∽△CED，根据相似三角形的性质即可求得结果.
（1）
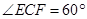
（2）
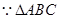是等边三角形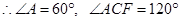
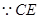平分
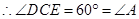
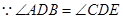
∴△ABD∽△CED；
（3）作B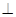GAC于G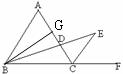 
则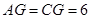
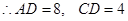
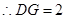
可求得BG=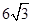
由（1）得△ABD∽△CED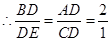
.
考点：等边三角形的性质，角平分线的性质，勾股定理，相似三角形的判定和性质
点评：解答本题的关键是读懂题意及图形，正确作出辅助线，同时熟练掌握相似三角形的对应边对应成比例，注意对应字母在对应位置上.
练习册系列答案
七彩题卡口算应用一点通系列答案
相关题目
6、已知：如图△ABC是等边三角形，过AB边上的点D作DG∥BC，交AC于点G，在GD的延长线上取点E，使DE=DB，连接AE、CD．
如图△ABC是等边三角形，BD是中线，延长BC到E，使CE=CD．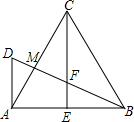
如图CE是等边三角形ABC边AB边上的高，AB=4，DA⊥AB，DA=
如图△AOB是等边三角形，点B的坐标为（4，0），则点A关于y轴的对称点A′的坐标为