题目内容
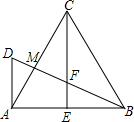如图CE是等边三角形ABC边AB边上的高，AB=4，DA⊥AB，DA=| 3 |
（1）求CF的长；
（2）求△ABM的面积．
分析：（1）利用三角形的中位线平行于第三边并且等于它的一半可求得EF的长，则CF的长可求；
（2）由（1）中过程可知△ADM∽△CFM，根据相似比可求出AM的长，过点M作MN⊥AB于N，在Rt△AMN中可求出高MN的长，则△ABM的面积可求解．
（2）由（1）中过程可知△ADM∽△CFM，根据相似比可求出AM的长，过点M作MN⊥AB于N，在Rt△AMN中可求出高MN的长，则△ABM的面积可求解．
解答：解：（1）∵CE是等边三角形ABC边AB上的高，
∴E是AB的中点，
∵DA⊥AB，∴CE∥DA，
∵DA=
，∴EF=
AD=
，
∴AB=4，∴CE=2
，
∴CF=CE-EF=
；
（2）如图，过点M作MN⊥AB于点N，
∵△ADM∽△CFM，∴
=
=
，
∴
=
，
∴AM=
AC=
，
在Rt△AMN中，
∵AM=
，∠MAB=60°，
∴MN=AM•sin60°=
，
∴S△ABM=
AB•MN=
．
∴E是AB的中点，
∵DA⊥AB，∴CE∥DA，
∵DA=
| 3 |
| 1 |
| 2 |
| ||
| 2 |
∴AB=4，∴CE=2
| 3 |
∴CF=CE-EF=
3
| ||
| 2 |
（2）如图，过点M作MN⊥AB于点N，
∵△ADM∽△CFM，∴
| AM |
| MC |
| AD |
| CF |
| 2 |
| 3 |
∴
| AM |
| AC |
| 2 |
| 5 |
∴AM=
| 2 |
| 5 |
| 8 |
| 5 |
在Rt△AMN中，
∵AM=
| 8 |
| 5 |
∴MN=AM•sin60°=
4
| ||
| 5 |
∴S△ABM=
| 1 |
| 2 |
8
| ||
| 5 |
点评：本题考查了三角形的中位线定理、等边三角形的性质及相似三角形的性质及判定．相似比是联系周长、面积、对应线段等的媒介，也是相似三角形计算中常用的一个比值．
练习册系列答案
相关题目
,BD与CE、CA分别交于点F、M .（1）求CF的长；（2）求△ABM的面积。
，BD与CE、CA分别交于点F、M．
，BD与CE、CA分别交于点F、M．
，BD与CE、CA分别交于点F、M．