题目内容
【题目】平面直角坐标系xOy中,横坐标为a的点A在反比例函数y1═![]() (x>0)的图象上,点A′与点A关于点O对称,一次函数y2=mx+n的图象经过点A′.
(x>0)的图象上,点A′与点A关于点O对称,一次函数y2=mx+n的图象经过点A′.
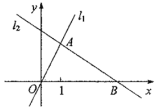
(1)设a=2,点B(4,2)在函数y1、y2的图象上.
①分别求函数y1、y2的表达式;
②直接写出使y1>y2>0成立的x的范围;
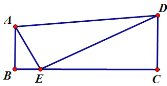
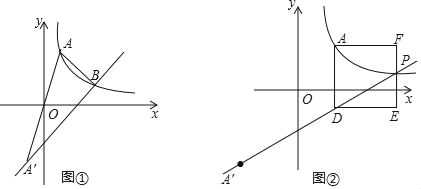
(2)如图①,设函数y1、y2的图象相交于点B,点B的横坐标为3a,△AA'B的面积为16,求k的值;
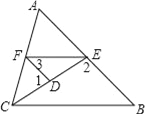
(3)设m=![]() ,如图②,过点A作AD⊥x轴,与函数y2的图象相交于点D,以AD为一边向右侧作正方形ADEF,试说明函数y2的图象与线段EF的交点P一定在函数y1的图象上.
,如图②,过点A作AD⊥x轴,与函数y2的图象相交于点D,以AD为一边向右侧作正方形ADEF,试说明函数y2的图象与线段EF的交点P一定在函数y1的图象上.
【答案】(1)y1=![]() ,y2=x﹣2;②2<x<4;(2)k=6;(3)证明见解析.
,y2=x﹣2;②2<x<4;(2)k=6;(3)证明见解析.
【解析】(1)由已知代入点坐标即可;
(2)面积问题可以转化为△AOB面积,用a、k表示面积问题可解;
(3)设出点A、A′坐标,依次表示AD、AF及点P坐标.
(1)①由已知,点B(4,2)在y1═![]() (x>0)的图象上
(x>0)的图象上
∴k=8
∴y1=![]()
∵a=2
∴点A坐标为(2,4),A′坐标为(﹣2,﹣4)
把B(4,2),A(﹣2,﹣4)代入y2=mx+n得,
![]() ,
,
解得![]() ,
,
∴y2=x﹣2;
②当y1>y2>0时,y1=![]() 图象在y2=x﹣2图象上方,且两函数图象在x轴上方,
图象在y2=x﹣2图象上方,且两函数图象在x轴上方,
∴由图象得:2<x<4;
(2)分别过点A、B作AC⊥x轴于点C,BD⊥x轴于点D,连BO,
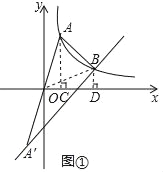
∵O为AA′中点,
S△AOB=![]() S△AOA′=8
S△AOA′=8
∵点A、B在双曲线上
∴S△AOC=S△BOD
∴S△AOB=S四边形ACDB=8
由已知点A、B坐标都表示为(a,![]() )(3a,
)(3a,![]() )
)
∴![]() ,
,
解得k=6;
(3)由已知A(a,![]() ),则A′为(﹣a,﹣
),则A′为(﹣a,﹣![]() ).
).
把A′代入到y=![]() ,得:﹣
,得:﹣![]() ,
,
∴n=![]() ,
,
∴A′B解析式为y=﹣![]() .
.
当x=a时,点D纵坐标为![]() ,
,
∴AD=![]()
∵AD=AF,
∴点F和点P横坐标为![]() ,
,
∴点P纵坐标为![]() .
.
∴点P在y1═![]() (x>0)的图象上.
(x>0)的图象上.