题目内容
为了解方程(x2-1)2-5(x2-1)+4=0时,我们可以将x2-1看成一个整体,设x2-1=y,则(x2-1)2=y2,
原方程可化为y2-5y+4=0,
解得y1=1,y2=4.
当y=1时,即x2-1=1解得x=±
当y=4时,即x2-1=4,解得x=±
∴原方程的解为x1=
,x2=-
,y1=
,y2=-
阅读上述材料,利用上面方程的解法解方程:x4-2x2-3=0.
原方程可化为y2-5y+4=0,
解得y1=1,y2=4.
当y=1时,即x2-1=1解得x=±
| 2 |
当y=4时,即x2-1=4,解得x=±
| 5 |
∴原方程的解为x1=
| 2 |
| 2 |
| 5 |
| 5 |
阅读上述材料,利用上面方程的解法解方程:x4-2x2-3=0.
考点:换元法解一元二次方程
专题:阅读型
分析:阅读题干中给出方程的求解方法,我们可以把x2当作一个整体,设x2=y,则y>0,原式可化简为y2-2y-3=0,即可求得y的值,根据y>0即可求得x的值,即可解题.
解答:解:设x2=y,则(x2)2=y2,
∴原方程x4-2x2-3=0,
可化简为:y2-2y-3=0,
解得:y1=3,y2=-1,
∵y=x2,∴y2不符合题意,舍去,
∴y=3,即x2=3解得x=±
.
∴原方程的解为x1=
,x2=-
.
∴原方程x4-2x2-3=0,
可化简为:y2-2y-3=0,
解得:y1=3,y2=-1,
∵y=x2,∴y2不符合题意,舍去,
∴y=3,即x2=3解得x=±
| 3 |
∴原方程的解为x1=
| 3 |
| 3 |
点评:本题考查了换元法求解一元二次方程的方法,换元法就是把多项式看作一个整体把原式化简成一个一元二次方程,然后再求解看作整体的多项式即可解题.

练习册系列答案
相关题目
 如图,在等边三角形ABC中,D是BC边上的任一点,延长AD至点E,使AE=AB,作∠BAE的平分线交△ABC的高BF于点O,连接OE,求证:无论点D在BC上如何运动(端点B除外),∠AEO均为30°.
如图,在等边三角形ABC中,D是BC边上的任一点,延长AD至点E,使AE=AB,作∠BAE的平分线交△ABC的高BF于点O,连接OE,求证:无论点D在BC上如何运动(端点B除外),∠AEO均为30°.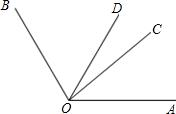 已知∠BOC=2∠AOC,OD平分∠AOB,∠AOC=35°,求∠COD的度数.
已知∠BOC=2∠AOC,OD平分∠AOB,∠AOC=35°,求∠COD的度数.