题目内容
 如图,在等边三角形ABC中,D是BC边上的任一点,延长AD至点E,使AE=AB,作∠BAE的平分线交△ABC的高BF于点O,连接OE,求证:无论点D在BC上如何运动(端点B除外),∠AEO均为30°.
如图,在等边三角形ABC中,D是BC边上的任一点,延长AD至点E,使AE=AB,作∠BAE的平分线交△ABC的高BF于点O,连接OE,求证:无论点D在BC上如何运动(端点B除外),∠AEO均为30°.考点:全等三角形的判定与性质,等边三角形的性质
专题:
分析:易证∠BAO=∠EAO,即可证明△BAO≌△EAO,可得∠AEO=∠ABO,易证∠ABO=30°,即可解题.
解答:证明:∵AO平分∠BAE,
∴∠BAO=∠EAO,
∵在△BAO和△EAO中,
,
∴△BAO≌△EAO,(SAS)
∴∠AEO=∠ABO,
∵BF⊥AC,∴∠ABO=30°,
∴∠AEO=30°,
故无论点D在BC上如何运动(端点B除外),∠AEO均为30°.
∴∠BAO=∠EAO,
∵在△BAO和△EAO中,
|
∴△BAO≌△EAO,(SAS)
∴∠AEO=∠ABO,
∵BF⊥AC,∴∠ABO=30°,
∴∠AEO=30°,
故无论点D在BC上如何运动(端点B除外),∠AEO均为30°.
点评:本题考查了全等三角形的判定,考查了全等三角形对应角相等的性质,本题中求证△BAO≌△EAO是解题的关键.

练习册系列答案
相关题目
如果把分式
中的x和y都扩大3倍,那么分式的值( )
| x |
| x+y |
| A、不变 | B、缩小3倍 |
| C、扩大3倍 | D、扩大9倍 |
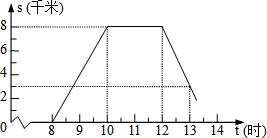 某班师生组织植树活动,上午8时从学校出发,到植树地点植树后原路匀速返回学校,如图为师生距离学校的路程s与时间t之间的图象.师生( )时回到学校.
某班师生组织植树活动,上午8时从学校出发,到植树地点植树后原路匀速返回学校,如图为师生距离学校的路程s与时间t之间的图象.师生( )时回到学校.| A、13 | B、13.4 |
| C、13.6 | D、14 |
 请把如图中的十字用四条线段把它分割,并把分割后的图形组合成一个正方形画出来.
请把如图中的十字用四条线段把它分割,并把分割后的图形组合成一个正方形画出来.
 如果一个等腰三角形两腰上的中线互相垂直,其中底边为4,那么这个三角形的面积是
如果一个等腰三角形两腰上的中线互相垂直,其中底边为4,那么这个三角形的面积是