题目内容
6. 如图,已知∠1=70°,如果CD∥BE,那么∠B的度数为( )
如图,已知∠1=70°,如果CD∥BE,那么∠B的度数为( )| A. | 70° | B. | 100° | C. | 110° | D. | 12° |
分析 先求出∠1的对顶角,再根据两直线平行,同旁内角互补即可求出.
解答  解:如图,∵∠1=70°,
解:如图,∵∠1=70°,
∴∠2=∠1=70°,
∵CD∥BE,
∴∠B=180°-∠1=180°-70°=110°.
故答案是:110°.
点评 本题考查了平行线的性质的应用,能根据平行线的性质求出∠B=∠AMD是解此题的关键,注意:两直线平行,同位角相等.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17. 如图,线段AC上有两点E、F,已知AE=CF,FM∥EN,点D在FM上,连接AD构成△AFD,点B在EN上,连接CB构成△CEB,那么添加下列一个条件后,无法判定△ADF≌△CBE的是( )
如图,线段AC上有两点E、F,已知AE=CF,FM∥EN,点D在FM上,连接AD构成△AFD,点B在EN上,连接CB构成△CEB,那么添加下列一个条件后,无法判定△ADF≌△CBE的是( )
 如图,线段AC上有两点E、F,已知AE=CF,FM∥EN,点D在FM上,连接AD构成△AFD,点B在EN上,连接CB构成△CEB,那么添加下列一个条件后,无法判定△ADF≌△CBE的是( )
如图,线段AC上有两点E、F,已知AE=CF,FM∥EN,点D在FM上,连接AD构成△AFD,点B在EN上,连接CB构成△CEB,那么添加下列一个条件后,无法判定△ADF≌△CBE的是( )| A. | ∠FAD=∠ECB | B. | AD=CB | C. | BE=DF | D. | AD∥BC |
18.下列说法正确的是( )
| A. | 不相交的两条直线是平行线 | |
| B. | 经过一点有且只有一条直线与已知直线平行 | |
| C. | 若直线a平行于直线b,直线b平行于直线c,则直线a平行于直线c | |
| D. | 没有公共点的两条直线平行 |
15.下列说法不一定正确的是( )
| A. | 平分弦和这条弦所对的弧的直线必过圆心 | |
| B. | 相等的弧所对的弦相等 | |
| C. | 直径所对的弧是半圆 | |
| D. | 垂直于半径的直线是圆的切线 |
 如图,在△ABC中,∠C是钝角,完成下列画图,并用适当的语言表述.
如图,在△ABC中,∠C是钝角,完成下列画图,并用适当的语言表述.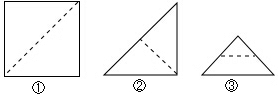 小麦拿了一张正方形纸(如图①),沿虚线对折一次得②,再对折一次得③,然后用剪刀沿图③中的虚线(虚线与底边平行)剪去一个角,再打开后的形状应是( )
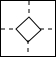
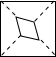
小麦拿了一张正方形纸(如图①),沿虚线对折一次得②,再对折一次得③,然后用剪刀沿图③中的虚线(虚线与底边平行)剪去一个角,再打开后的形状应是( )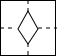
 如图,是用相同的小正方体搭成的几何体,从几何体的上面看得到的平面图形是( )
如图,是用相同的小正方体搭成的几何体,从几何体的上面看得到的平面图形是( )



 如图所示,以?ABCD的顶点A为圆心,AB为半径作圆,分别交AD,BC于点E,F,延长BA交⊙A于G.
如图所示,以?ABCD的顶点A为圆心,AB为半径作圆,分别交AD,BC于点E,F,延长BA交⊙A于G.