题目内容
16．小明同学先向北行进4千米，然后向东进4千米，再向北行进2千米，最后又向东行进一定距离，此时小明离出发点的距离是10千米，小明最后向东行进了（ ）| A． | 3千米 | B． | 4千米 | C． | 5千米 | D． | 6千米 |
分析 根据题意画出图形，进而得出各边长，再利用结合勾股定理得出答案．
解答 
解：如图所示：由题意可得，AE=10km，AF=6km，
则在Rt△AFE中，
EF=$\sqrt{A{E}^{2}-A{F}^{2}}$=8（km），
∵BC=4km，则DE=8-4=4（km），
故选：B．
点评 此题主要考查了勾股定理的应用，正确理解题意画出图形是解题关键．
练习册系列答案
云南师大附小一线名师提优作业系列答案
冲刺100分单元优化练考卷系列答案
相关题目
如图，已知线段AB=a．
7．27的立方根是（ ）
| A． | -3 | B． | -9 | C． | 3 | D． | 9 |
4．
如图，直线l1∥l2∥l3，直线AC分别交l1，l2，l3于点A，B，C；直线DF分别交l1，l2，l3于点D、E、F，AC与DF相交于点H，且AH=2，HB=1，BC=5，则$\frac{DE}{EF}$=（ ）
如图，直线l1∥l2∥l3，直线AC分别交l1，l2，l3于点A，B，C；直线DF分别交l1，l2，l3于点D、E、F，AC与DF相交于点H，且AH=2，HB=1，BC=5，则$\frac{DE}{EF}$=（ ）| A． | $\frac{3}{5}$ | B． | 2 | C． | $\frac{2}{5}$ | D． | $\frac{1}{2}$ |
11．△ABC与△DEF的相似比为1：4，则△ABC与△DEF的周长比为（ ）
| A． | 1：4 | B． | 1：3 | C． | 1：2 | D． | 1：16 |
1．
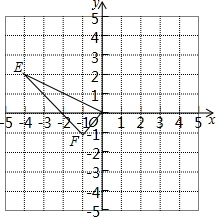如图所示，E（-4，2），F（-1，-1），以O为位似中心，按比例1：2把△EFO缩小，则点E的对应点E′的坐标为（ ）
如图所示，E（-4，2），F（-1，-1），以O为位似中心，按比例1：2把△EFO缩小，则点E的对应点E′的坐标为（ ）| A． | （2，-1）或（-2，1） | B． | （8，-4）或（-8，4） | C． | （2，-1） | D． | （8，-4） |
8．如果（ ）×（-$\frac{2}{3}$）=-1，则括号内应填的数是（ ）
| A． | $\frac{3}{2}$ | B． | $\frac{2}{3}$ | C． | C-$\frac{2}{3}$ | D． | -$\frac{3}{2}$ |
5．已知x=1是一元二次方程x2-2ax+1=0的一个根，则a的值是（ ）
| A． | $\frac{1}{2}$ | B． | 0 | C． | 2或-2 | D． | 1 |
6．某药品经过两次降价，每瓶零售价由200元降为128元．已知两次降价的百分率相同，每次降价的百分率为x，根据题意列方程得（ ）
| A． | 200（1+x）2=128 | B． | 200（1-x）2=128 | C． | 128（1+x）2=200 | D． | 200（1-x2）=128 |