题目内容
13.有一列按一定顺序和规律排列的数:第一个数是$\frac{1}{1×2}$;
第二个数是$\frac{1}{2×3}$;
第三个数是$\frac{1}{3×4}$;
…
(1)经过探究,我们发现:$\frac{1}{1×2}$=$\frac{1}{1}$-$\frac{1}{2}$,$\frac{1}{2×3}$=$\frac{1}{2}-\frac{1}{3}$,$\frac{1}{3×4}$=$\frac{1}{3}-\frac{1}{4}$,设这列数的第5个数为a,那么a>$\frac{1}{5}$-$\frac{1}{6}$,a=$\frac{1}{5}$-$\frac{1}{6}$,a<$\frac{1}{5}$-$\frac{1}{6}$,哪个正确?请你直接写出正确的结论:
(2)计算:$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{n(n+1)}$;
(3)设M=$\frac{1}{{2}^{2}}$+$\frac{1}{{3}^{2}}$+$\frac{1}{{4}^{2}}$+…+$\frac{1}{201{7}^{2}}$,求证:$\frac{504}{1009}$<M<$\frac{2016}{2017}$.
分析 (1)根据题意可以判断哪个结论正确;
(2)根据题意可以计算出所求式子的结果;
(3)根据题意可以利用前面的结论证明结论成立.
解答 解:(1)由题意可得,
第5个数为a=$\frac{1}{5}$-$\frac{1}{6}$正确;
(2)$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{n(n+1)}$
=$1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+…+\frac{1}{n}-\frac{1}{n+1}$
=1-$\frac{1}{n+1}$
=$\frac{n}{n+1}$;
(3)证明:∵$\frac{1}{2×3}<\frac{1}{{2}^{2}}<\frac{1}{1×2}$,
$\frac{1}{3×4}<\frac{1}{{3}^{2}}<\frac{1}{2×3}$,
…
$\frac{1}{2017×2018}<\frac{1}{201{7}^{2}}<\frac{1}{2017×2016}$,
∴$\frac{1}{2×3}+\frac{1}{3×4}+…+\frac{1}{2017×2018}<M<$$\frac{1}{1×2}+\frac{1}{2×3}+…+\frac{1}{2016×2017}$,
∴$\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+…+\frac{1}{2017}-\frac{1}{2018}<M<$$1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+…+\frac{1}{2016}-\frac{1}{2017}$,
∴$\frac{1}{2}-\frac{1}{2018}<M<1-\frac{1}{2017}$,
∴$\frac{504}{1009}<M<\frac{2016}{2017}$.
点评 本题考查分式的混合运算、数字的变化类,解题的关键是明确题意,找出所求问题需要的条件.

 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案| A. | 1,2,1 | B. | 1,2,3 | C. | 1,2,2 | D. | 1,2,4 |
| A. | 12 cm | B. | 8 cm | C. | 12 cm或8 cm | D. | 以上均不对 |
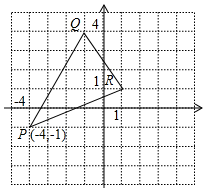 如图,请作出△PQR关于y轴对称的△P1Q1R1,并写出△P1Q1R1三个顶点的坐标.
如图,请作出△PQR关于y轴对称的△P1Q1R1,并写出△P1Q1R1三个顶点的坐标.