题目内容
解不等式（组）
（1）解不等式
≥
，并把解集在数轴上表示出来．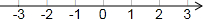
（2）解不等式组
，并写出它的所有整数解．
（1）解不等式
| 4+3x |
| 6 |
| 1+2x |
| 3 |
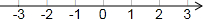
（2）解不等式组
|
考点：解一元一次不等式组,在数轴上表示不等式的解集,解一元一次不等式,一元一次不等式组的整数解
专题：
分析：（1）去分母、去括号，然后移项、合并同类项，系数化成1即可求解；
（2）先求出不等式组中每一个不等式的解集，再求出它们的公共部分，然后把不等式的解集表示在数轴上即可．
（2）先求出不等式组中每一个不等式的解集，再求出它们的公共部分，然后把不等式的解集表示在数轴上即可．
解答：解：（1）去分母，得：3（4+3x）≥6（1+2x），
去括号，得：12+9x≥6+12x，
移项，得：9x-12x≥6-12，
合并同类项，得：-3x≥-6，
系数化成1得：x≤2．
解集在数轴上表示出来为：
；
（2）
，
解①得：x≤2，
解②得：x＞-1．
解集在数轴上表示出来为：
，
则整数解是：0，1，2．
去括号，得：12+9x≥6+12x，
移项，得：9x-12x≥6-12，
合并同类项，得：-3x≥-6，
系数化成1得：x≤2．
解集在数轴上表示出来为：
；（2）
|
解①得：x≤2，
解②得：x＞-1．
解集在数轴上表示出来为：
，则整数解是：0，1，2．
点评：本题考查的是一元一次不等式组的解，解此类题目常常要结合数轴来判断．还可以观察不等式的解，若x＞较小的数、＜较大的数，那么解集为x介于两数之间．
练习册系列答案
天天向上口算本系列答案
相关题目
如图，一只蚂蚁从A沿圆柱表面爬到B处，如果圆柱的高为8cm，圆柱的底面半径为下列运算中，正确的是（ ）
| A、ab2÷a=b2 |
| B、a2+a3=a5 |
| C、（-2a）3=-6a3 |
| D、3a-a=3 |
两个有理数的和（ ）
| A、一定大于其中的一个加数 |
| B、一定小于其中的一个加数 |
| C、和的大小由两个加数的符号而定 |
| D、和的大小由两个加数的绝对值而定 |
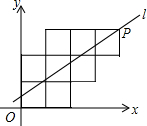八个边长为1的正方形如图摆放在平面直角坐标系中，经过P点的一条直线l将这八个正方形分成面积相等的两部分，则该直线l的解析式为（ ）A、y=
| ||||
B、y=
| ||||
C、y=
| ||||
D、y=
|
小张把两个大小不同的苹果放到天平上称，当天平保持平衡时的砝码重量如图所示．问：这两个苹果的重量分别为多少g？