题目内容
在一个不透明的布袋中,装有三个小球,小球上分别标有数字“1”、“2”和“3”,它们除了数字不同外,其余都相同.
(1)随机地从布袋中摸出一个小球,则摸出的球为“3”的概率是多少?
(2)若第一次从布袋中随机摸出一个小球,设记下的数字为x,再将此球放回盒中,第二次再从布袋中随机抽取一张,设记下的数字为y,请用画树状图或列表法表示出上述情况的所有等可能结果,并求出x+y>3的概率.
(1)随机地从布袋中摸出一个小球,则摸出的球为“3”的概率是多少?
(2)若第一次从布袋中随机摸出一个小球,设记下的数字为x,再将此球放回盒中,第二次再从布袋中随机抽取一张,设记下的数字为y,请用画树状图或列表法表示出上述情况的所有等可能结果,并求出x+y>3的概率.
考点:列表法与树状图法
专题:
分析:(1)直接利用概率公式求解即可;
(2)用列表或树状图将所有等可能的结果列举出来即可利用概率公式直接求解.
(2)用列表或树状图将所有等可能的结果列举出来即可利用概率公式直接求解.
解答:解:(1)∵三个小球中有一个标有数字3,
所以摸出的球为3的概率为:
;
(2)(解法一)列举所有等可能结果,画出树状图如下:

由上图可知,共有9种等可能结果,其中x+y>3的情况有6种.
∴P(x+y>3)=
=
;
(解法二)(1)列表如下
由上图可知,共有9种等可能结果,其中x+y>3的情况有6种.
∴P(x+y>3)=
=
;
所以摸出的球为3的概率为:
| 1 |
| 3 |
(2)(解法一)列举所有等可能结果,画出树状图如下:

由上图可知,共有9种等可能结果,其中x+y>3的情况有6种.
∴P(x+y>3)=
| 6 |
| 9 |
| 2 |
| 3 |
(解法二)(1)列表如下
| 数字x 和 |
1 | 2 | 3 |
| 1 | 2 | 3 | 4 |
| 2 | 3 | 4 | 5 |
| 3 | 4 | 5 | 6 |
∴P(x+y>3)=
| 6 |
| 9 |
| 2 |
| 3 |
点评:本题考查了列表或列树状图的方法求概率,解题的关键是能够将所有等可能的结果正确的列举出来,难度不大.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
 如图,在?ABCD中,点E、点F分别在AD、CB的延长线上,且DE=BF,连结EF分别交AB、CD于点H、点G.
如图,在?ABCD中,点E、点F分别在AD、CB的延长线上,且DE=BF,连结EF分别交AB、CD于点H、点G.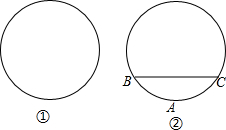 某市新建了圆形文化广场,小杰和小浩准备用不同的方法测量该广场的半径.
某市新建了圆形文化广场,小杰和小浩准备用不同的方法测量该广场的半径. 如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC,设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC,设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.