题目内容
15.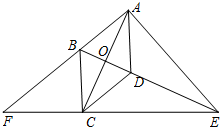 菱形ABCD中,∠BAD是锐角,AC,BD相交于点O,E是BD的延长线上一动点(不与点D重合),连接EC并延长和AB的延长线交于点F,连接AE.
菱形ABCD中,∠BAD是锐角,AC,BD相交于点O,E是BD的延长线上一动点(不与点D重合),连接EC并延长和AB的延长线交于点F,连接AE.(1)比较∠F和∠ABD的大小,并说明理由;
(2)当△BFC有一个内角是直角时,△BFC与△EFA是否相似,请说明理由.
分析 (1)根据三角形外角的性质即可得出结论;
(2)推出这个直角为∠BCF,然后证明△△ABE≌△CBE,得出∠FCB=∠FAE=90°,即可证明结论.
解答 解:(1)∠ABD>∠F;理由如下:
∵∠ABD为△BFE的一个外角,
∴∠ABD>∠F;
(2)△BFC∽△EFA;理由如下:
∵四边形ABCD是菱形,
∴BC∥AD,∠ABD=$\frac{1}{2}$∠ABC,BA=BC,
∴∠BAD=∠FBC,∠BAD+∠ABC=180°
又∵∠BAD为锐角,
∴∠FBC为锐角,∠ABC为钝角,
∴∠ABD为锐角,
由(1)得:∠F也为锐角,
又∵△BFC有一个角是直角,
∴∠BCF为直角,
在△ABE和△CBE中,
$\left\{\begin{array}{l}{BA=BC}&{\;}\\{∠ABE=∠CBE}&{\;}\\{BE=BE}&{\;}\end{array}\right.$,
∴△ABE≌△CBE,
∴∠BAE=∠BCE=90°,
∴∠FCB=∠FAE=90°,
∴△BFC∽△EFA.
点评 本题考查了相似三角形的判定与性质、菱形的性质以及全等三角形的判定与性质;特别是(2)中,证明三角形全等得出角相等是解决问题的关键.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
6.已知m-2n=-1,则代数式1-2m+4n的值是( )
| A. | -3 | B. | -1 | C. | 2 | D. | 3 |
3.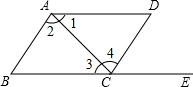 如图,点E在BC的延长线上,下列条件中能判断AB∥CD的是( )
如图,点E在BC的延长线上,下列条件中能判断AB∥CD的是( )
 如图,点E在BC的延长线上,下列条件中能判断AB∥CD的是( )
如图,点E在BC的延长线上,下列条件中能判断AB∥CD的是( )| A. | ∠1=∠3 | B. | ∠D=∠DCE | C. | ∠2=∠4 | D. | ∠D+∠BCD=180° |
 如图,△ABC是以BC为底边的等腰三角形,点A、C分别是一次函数y=-$\frac{3}{4}$x+3的图象与y轴、x轴的交点,点B在二次函数y=$\frac{1}{8}$x2+bx+c的图象上,且该二次函数图象上存在一点D使四边形ABCD能构成平行四边形.
如图,△ABC是以BC为底边的等腰三角形,点A、C分别是一次函数y=-$\frac{3}{4}$x+3的图象与y轴、x轴的交点,点B在二次函数y=$\frac{1}{8}$x2+bx+c的图象上,且该二次函数图象上存在一点D使四边形ABCD能构成平行四边形. 如图是一束平行光线从教室窗户射入的平面示意图,BC=1,NC=$\frac{4}{3}$,BN=$\frac{5}{3}$,AB=3.5,MN=$\frac{14}{3}$,求AM的长度.
如图是一束平行光线从教室窗户射入的平面示意图,BC=1,NC=$\frac{4}{3}$,BN=$\frac{5}{3}$,AB=3.5,MN=$\frac{14}{3}$,求AM的长度.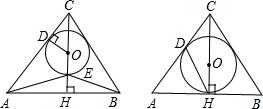
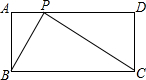 如图,在长方形ABCD中,AB=2$\sqrt{5}$cm,BC=4$\sqrt{5}$cm.点P以$\sqrt{5}$cm/s的速度在长方形边上从点A出发,沿A-D-C的路径运动,到点C停止.
如图,在长方形ABCD中,AB=2$\sqrt{5}$cm,BC=4$\sqrt{5}$cm.点P以$\sqrt{5}$cm/s的速度在长方形边上从点A出发,沿A-D-C的路径运动,到点C停止.