Question

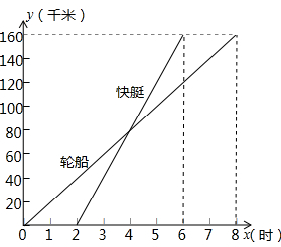如图表示一艘轮船和一艘快艇沿相同路线从甲港出发到乙港行驶过程中路程随时间变化的图象．根据图象解答下列问题：
（1）在轮船快艇中，哪一个的速度较大？分别是多少？
（2）快艇出发后几个小时与轮船相遇？
（3）回答：当时间x在什么范围内时，快艇在轮船的后面？当时间x在什么范围内时，快艇在轮船的前面？

Answer 1

考点：一次函数的应用

专题：

分析：（1）根据速度=路程÷时间分别列式计算即可得解；
（2）设快艇出发x小时与轮船相遇，然后根据追及问题等量关系列出方程求解即可；
（3）先求出轮船与快艇相遇的时间，再根据函数图象分别写出x的取值范围即可．

解答：解：（1）轮船速度：160÷8=20千米/时，
快艇速度；160÷（6-2）=40千米/时，
∵20＜40，
∴快艇的速度大；

（2）设快艇出发x小时与轮船相遇，
由题意得，40x=20（x+2），
解得x=2，
答：快艇出发后2小时与轮船相遇；

（3）轮船与快艇相遇的时间为2+2=4小时，
所以，0≤x＜4时，快艇在轮船的后面，4＜x＜8时，快艇在轮船的前面．

点评：本题考查了一次函数的应用，主要利用了路程、时间、速度三者之间的关系，追及问题的等量关系，准确识图获取必要的信息是解题的关键．