题目内容
4.已知:顺次连接矩形各边的中点,得到一个菱形,如图①;再顺次连接菱形各边的中点,得到一个新的矩形,如图②;然后顺次连接新的矩形各边的中点,得到一个新的菱形,如图③;如此反复操作下去,则第2014个图形中直角三角形的个数有( )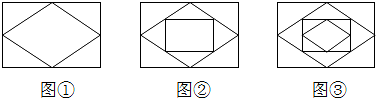
| A. | 2014个 | B. | 2015个 | C. | 4028个 | D. | 6042个 |
分析 观察图形可知,两个图形为一个组,直角三角形的个数相同,且都是4的倍数,然后求出第2013个图形的组数,计算即可得解.
解答 解:图①、图②的直角三角形的个数相同,都是4,4=4×1,
图③、图④的直角三角形的个数相同,都是8,8=4×2,
…,
图2013、图2014的直角三角形的个数相同,都是4×$\frac{2014}{2}$=4028.
故选:C.
点评 本题是对中点四边形,图形变化规律的考查,观察图形,得到两个图形的直角三角形的个数相同是解题的关键.

练习册系列答案
相关题目
9.一元二次方程x2-9x+18=0的两根是一等腰三角形的底和腰,则这个等腰三角形的周长为( )
| A. | 12 | B. | 12或15 | C. | 15 | D. | 无法确定 |
16. 如图,AB∥CD,下列结论中错误的是( )
如图,AB∥CD,下列结论中错误的是( )
 如图,AB∥CD,下列结论中错误的是( )
如图,AB∥CD,下列结论中错误的是( )| A. | ∠1=∠2 | B. | ∠2+∠5=180° | C. | ∠2+∠3=180° | D. | ∠3+∠4=180° |
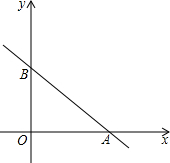 在平面直角坐标系中,一次函数的图象与坐标轴围成的三角形,叫做此一次函数的坐标三角形.例如,图中的一次函数的图象与x,y轴分别交于点A,B,则△OAB为此函数的坐标三角形.求函数y=-$\frac{3}{4}$x+3的坐标三角形的三条边长.
在平面直角坐标系中,一次函数的图象与坐标轴围成的三角形,叫做此一次函数的坐标三角形.例如,图中的一次函数的图象与x,y轴分别交于点A,B,则△OAB为此函数的坐标三角形.求函数y=-$\frac{3}{4}$x+3的坐标三角形的三条边长. 如图,点C是线段AB的中点,点D是线段AC上的一点,且DC=2AD,若DC=16cm,求线段DB的长度.
如图,点C是线段AB的中点,点D是线段AC上的一点,且DC=2AD,若DC=16cm,求线段DB的长度.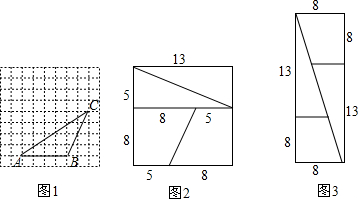
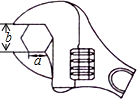 如图,要拧开一个正六边形螺帽,已知扳手张开的开口b长为2cm,螺帽的边长为a为$\frac{2\sqrt{3}}{3}$cm.
如图,要拧开一个正六边形螺帽,已知扳手张开的开口b长为2cm,螺帽的边长为a为$\frac{2\sqrt{3}}{3}$cm.