题目内容
18.如图所示,在△ABC中,BP和CP是角平分线,两线交于点P,试探求下列各图中∠A与∠P之间的关系,并选择一个加以证明.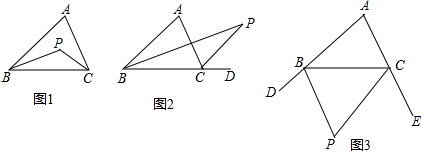
(1)图1中∠P与∠A之间的关系:∠P=90°+$\frac{1}{2}$∠A;
(2)图1中∠P与∠A之间的关系:∠P=$\frac{1}{2}$∠A;
(3)图1中∠P与∠A之间的关系:∠P=90°-$\frac{1}{2}$∠A.
分析 (1)根据角平分线的定义得出∠PBC=$\frac{1}{2}$∠ABC,∠PCB=$\frac{1}{2}$∠ACB,根据三角形内角和定理得出∠A+∠ABC+∠ACB=180°,求出∠PBC+∠PCB=$\frac{1}{2}$(∠ABC+∠ACB)=90°-$\frac{1}{2}$∠A,根据三角形内角和定理求出即可;
(2)根据角平分线定义得出∠ACD=2∠PCD,∠ABC=2∠PBC,根据三角形外角性质得出∠PCD=∠P+∠PBC,∠ACD=∠A+∠ABC,求出∠ACD=2∠PCD=2∠P+∠ABC,即可得出答案;
(3)根据角平分线定义得出∠PBC=$\frac{1}{2}$∠DBC,∠PCB=$\frac{1}{2}$∠ECB,求出∠DBC+∠ECB=180°+∠A,求出∠PBC+∠PCB=$\frac{1}{2}$(∠ABC+∠ACB=90°+$\frac{1}{2}$∠A,根据三角形内角和定理求出即可.
解答 解:(1)∠P=90°+$\frac{1}{2}$∠A,
理由是:∵BP和CP是角平分线,
∴∠PBC=$\frac{1}{2}$∠ABC,∠PCB=$\frac{1}{2}$∠ACB,
∵∠A+∠ABC+∠ACB=180°,
∴∠PBC+∠PCB=$\frac{1}{2}$(∠ABC+∠ACB)=$\frac{1}{2}$(180°-∠A)=90°-$\frac{1}{2}$∠A,
∴∠P=180°-(∠PBC+∠PCB)
=180°-(90°-$\frac{1}{2}$∠A)
=90°+$\frac{1}{2}$∠A,
故答案为:∠P=90°+$\frac{1}{2}$∠A;
(2)∠A=2∠P
理由是:∵BP、CP分别平分∠ABC和∠ACD,
∴∠ACD=2∠PCD,∠ABC=2∠PBC,
∵∠PCD=∠P+∠PBC,∠ACD=∠A+∠ABC,
∴∠ACD=2∠PCD=2∠P+∠ABC,
∴∠A=2∠P,
即∠P=$\frac{1}{2}$∠A,
故答案为:∠P=$\frac{1}{2}$∠A;
(3)∠P=90°-$\frac{1}{2}$∠A,
理由是:∵BP、CP分别平分∠DBC、∠ECB,
∴∠PBC=$\frac{1}{2}$∠DBC,∠PCB=$\frac{1}{2}$∠ECB,
∴∠DBC+∠ECB=360°-(∠ABC+∠ACB)=360°-(180°-∠A)=180°+∠A,
∴∠PBC+∠PCB=$\frac{1}{2}$(∠ABC+∠ACB)=$\frac{1}{2}$(180°+∠A)=90°+$\frac{1}{2}$∠A,
∴∠P=180°-(∠PBC+∠PCB)
=180°-(90°+$\frac{1}{2}$∠A)
=90°-$\frac{1}{2}$∠A,
故答案为:∠P=90°-$\frac{1}{2}$∠A.
点评 本题考查了三角形内角和定理和三角形外角性质的应用,能熟练地运用定理进行推理是解此题的关键.

| A. | (-2,3) | B. | (2,3) | C. | (-2,-3) | D. | (2,-3) |
| A. | $\sqrt{{a}^{2}x+{a}^{3}y}$ | B. | $\sqrt{\frac{1}{3}}$ | C. | $\sqrt{18}$ | D. | $\sqrt{{a}^{2}-{b}^{2}}$ |
 两条直线被第三条直线所截,如图所示,图中∠1的内错角是( )
两条直线被第三条直线所截,如图所示,图中∠1的内错角是( )| A. | ∠5 | B. | ∠6 | C. | ∠7 | D. | ∠8 |
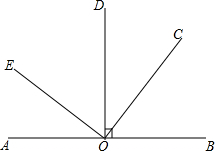 如图,直线AB上有一点O,∠DOB=90°,另有一顶点在O点的直∠EOC.
如图,直线AB上有一点O,∠DOB=90°,另有一顶点在O点的直∠EOC.