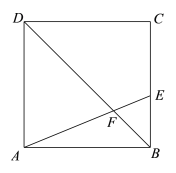
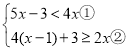题目内容
【题目】如图,![]() 为
为![]() 的直径,直线
的直径,直线![]() 与
与![]() 相切于点
相切于点![]() ,垂足为
,垂足为![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 若
若![]() ,则线段
,则线段![]() 的长为_________.
的长为_________.
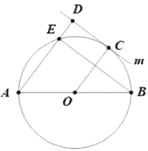
【答案】![]()
【解析】
设OC交BE于F,如图,有圆周角定理得到∠AEB=90°,加上AD⊥m,则可判断BE∥CD,再利用切线的性质得OC⊥CD,则OC⊥BE,原式可判断四边形CDEF为矩形,所以CD=EF,接着利用勾股定理计算出BE,然后利用垂径定理得到EF的长,从而得到CD的长.
解: 设OC交BE于F,如图,

∵AB为⊙O的直径,
∴∠AEB=90°,
∵AD⊥m,
∴BE∥CD,
∵CD为切线,
∴OC⊥CD,
∴OC⊥BE,
∴四边形CDEF为矩形,
∴CD=EF,
在Rt△ABE中,BE=![]() ,
,
∵OF⊥BE,
∴BF=EF=4,
∴CD=4.
故答案为:4.

练习册系列答案
相关题目