题目内容
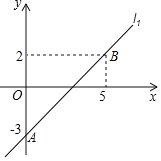
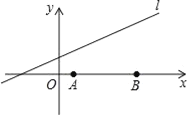
【题目】在平面直角坐标系中，二次函数抛物线
过点
和
，对称轴为直线
．
（1）求二次函数的表达式和顶点
的坐标．
（2）将抛物线在坐标平面内平移，使其过原点，若在平移后，第二象限的抛物线上存在点
，使
为等腰直角三角形，请求出抛物线平移后的表达式，并指出其中一种情况的平移方式．
【答案】（1）
，顶点
的坐标是
；（2）平移后抛物线表达式是
，
，
；原抛物线向左平移
个单位，再向下平移
个单位可得
【解析】
（1）可以采用待定系数法求二次函数的解析式，因为点A(-1,0)、C(0,-2)在函数图象上，对称轴为x=1，也可求得A的对称点的坐标为(3,0),列方程组即可求得解析式;
（2）根据平移后的图象过原点，所以设y =﹣x+bx，使抛物线第二象限上的点P与AB组成的△ABP是等腰直角三角形，所以分三种情况来讨论，分别求出三种情况的解析式．
（1）由题意，得
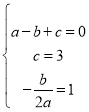，解得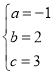
抛物线的表达式为；
当
时，
，顶点的坐标是
（2）平移后抛物线过原点，可设表达式是
，分三种情况：
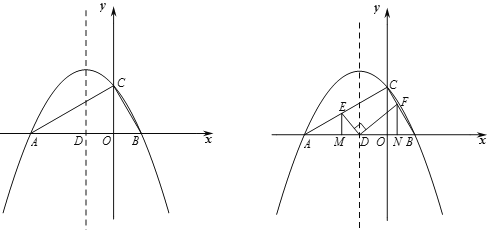
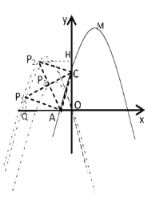
①当
为等腰直角三角形
的斜边，如图
所示，做
轴于
，
，
，
，
，又
，
，
，
，
，所以点坐标是
，
把
代入得，
，
．
所以平移后抛物线表达式是．
②当
为等腰直角三角形的斜边，如图
所示，
同上可得
，
，
，
所以点坐标是
，
把
代入得，
，
．
所以平移后抛物线表达式是．
③当
为等腰直角三角形的斜边，如图
所示，
这时是
的中点，因为，
，所以
，
把代入
得，
，
．
所以平移后抛物线表达式是．这时抛物线顶点是
，
可将原抛物线向左平移
个单位，再向下平移
个单位
综上所述，平移后抛物线表达式是，，；
原抛物线向左平移个单位，再向下平移个单位可得
练习册系列答案
期末1卷素质教育评估卷系列答案
相关题目
