题目内容
 如图,矩形ABCD,其面积为8,A、B为抛物线y=
如图,矩形ABCD,其面积为8,A、B为抛物线y=| 1 |
| 2 |
考点:二次函数图象上点的坐标特征
专题:计算题
分析:由A、B为抛物线y=
x2+bx+c上两点得到抛物线的对称轴为y轴,所以b=0,由抛物线的顶点在CD边上得到抛物线的顶点在原点,所以c=0,则抛物线的解析式为y=
x2,然后B点坐标为(a,
a2),利用矩形面积得到a•2•
a2=8,解得a=2,再确定矩形的长和宽.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:∵A、B为抛物线y=
x2+bx+c上两点,
∴抛物线的对称轴为y轴,即b=0,
∵抛物线的顶点在CD边上,
∴抛物线的顶点在原点,即c=0,
∴抛物线的解析式为y=
x2,
设B点坐标为(a,
a2),
∴a•2•
a2=8,
解得a=2,
∴矩形的长为4,宽为2.
| 1 |
| 2 |
∴抛物线的对称轴为y轴,即b=0,
∵抛物线的顶点在CD边上,
∴抛物线的顶点在原点,即c=0,
∴抛物线的解析式为y=
| 1 |
| 2 |
设B点坐标为(a,
| 1 |
| 2 |
∴a•2•
| 1 |
| 2 |
解得a=2,
∴矩形的长为4,宽为2.
点评:本题考查了二次函数图象上点的坐标特征:二次函数图象上点的坐标满足其解析式.也考查了二次函数的性质.

练习册系列答案
相关题目
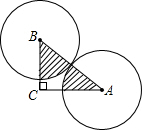 如图所示,在直角△中,C=90°,AC=6,BC=8,两等圆A,B外切,那么图中两个扇形(阴影部分)的面积之和( )
如图所示,在直角△中,C=90°,AC=6,BC=8,两等圆A,B外切,那么图中两个扇形(阴影部分)的面积之和( )A、
| ||
B、
| ||
C、
| ||
| D、25π |