题目内容
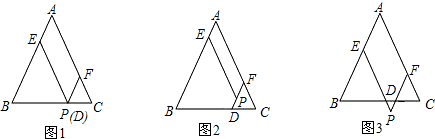
在△ABC中,AB=AC,点P△ABC为所在平面内一点,过点P分别作PE∥AC交AB于点E,PF∥AB交BC于点D,交AC于点F
(1)当点P在BC边上(如图1)时,请你探索线段PD,PE,PF,AB与之间的数量关系,并给出证明;
(2)当点P在△ABC内(如图2)时,(1)中的结论是否成立?若成立,请给出证明;若不成立,线段PD,PE,PF,AB与之间又有怎样的数量关系.
(3)当点P在△ABC外(如图3)时,线段PD,PE,PF,AB与之间又有怎样的数量关系.
(1)当点P在BC边上(如图1)时,请你探索线段PD,PE,PF,AB与之间的数量关系,并给出证明;
(2)当点P在△ABC内(如图2)时,(1)中的结论是否成立?若成立,请给出证明;若不成立,线段PD,PE,PF,AB与之间又有怎样的数量关系.
(3)当点P在△ABC外(如图3)时,线段PD,PE,PF,AB与之间又有怎样的数量关系.

考点:平行四边形的判定与性质,等腰三角形的性质
专题:
分析:(1)先求出四边形PFAE是平行四边形,根据平行四边形对边相等可得PF=AE,再根据两直线平行,同位角相等可得∠BPE=∠C,然后求出∠B=∠BPE,利用等角对等边求出PE=BE,然后求解即可;
(2)根据等边对等角可得∠B=∠C,再根据两直线平行,同位角相等可得∠B=∠CDF,然后求出∠C=∠CDF,再根据等角对等边可得CF=PD+PF,然后求出四边形PFAE是平行四边形,根据平行四边形对边相等可得PE=AF,然后求出PD+PE+PF=AC,等量代换即可得证;
(3)证明思路同(2).
(2)根据等边对等角可得∠B=∠C,再根据两直线平行,同位角相等可得∠B=∠CDF,然后求出∠C=∠CDF,再根据等角对等边可得CF=PD+PF,然后求出四边形PFAE是平行四边形,根据平行四边形对边相等可得PE=AF,然后求出PD+PE+PF=AC,等量代换即可得证;
(3)证明思路同(2).
解答:(1)答:PD+PE+PF=AB.
证明如下:∵点P在BC上,
∴PD=0,
∵PE∥AC,PF∥AB,
∴四边形PFAE是平行四边形,
∴PF=AE,
∵PE∥AC,
∴∠BPE=∠C,
∴∠B=∠BPE,
∴PE=BE,
∴PE+PF=BE+AE=AB,
∵PD=0,
∴PD+PE+PF=AB;
(2)证明:∵AB=AC,
∴∠B=∠C,
∵PF∥AB,
∴∠B=∠CDF,
∴∠C=∠CDF,
∴CF=PD+PF,
∵PE∥AC,PF∥AB,
∴四边形PFAE是平行四边形,
∴PE=AF,
∴PD+PE+PF=AC,
∴PD+PE+PF=AB;
(3)证明:同(2)可证DF=CF,PE=AF,
∵AF+CF=AC,
∴PE+PF-PD=AC,
∴PE+PF-PD=AB.
证明如下:∵点P在BC上,
∴PD=0,
∵PE∥AC,PF∥AB,
∴四边形PFAE是平行四边形,
∴PF=AE,
∵PE∥AC,
∴∠BPE=∠C,
∴∠B=∠BPE,
∴PE=BE,
∴PE+PF=BE+AE=AB,
∵PD=0,
∴PD+PE+PF=AB;
(2)证明:∵AB=AC,
∴∠B=∠C,
∵PF∥AB,
∴∠B=∠CDF,
∴∠C=∠CDF,
∴CF=PD+PF,
∵PE∥AC,PF∥AB,
∴四边形PFAE是平行四边形,
∴PE=AF,
∴PD+PE+PF=AC,
∴PD+PE+PF=AB;
(3)证明:同(2)可证DF=CF,PE=AF,
∵AF+CF=AC,
∴PE+PF-PD=AC,
∴PE+PF-PD=AB.
点评:本题考查了平行四边形的判定与性质,等腰三角形的性质,熟记平行四边形的判定方法与性质,并准确识图理清图中边的关系是解题的关键,此类题目,关键在于后面小题与前面小题的求解思路相同.

练习册系列答案
相关题目
某班为了解学生“多读书、读好书”活动的开展情况,对该班50名学生一周阅读课外书的时间进行了统计,统计结果如下:
由上表知,这50名学生一周阅读课外书时间的众数和中位数分别为( )
| 阅读时间(小时) | 1 | 2 | 3 | 4 | 5 |
| 人数(人) | 7 | 19 | 13 | 7 | 4 |
| A、2,3 |
| B、2,2 |
| C、19,19 |
| D、19; 13 |
 一次函数y=(k-2)x+b的图象如图所示,则k的取值范围是( )
一次函数y=(k-2)x+b的图象如图所示,则k的取值范围是( )| A、k>2 | B、k<2 |
| C、k>3 | D、k<3 |
 如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,-1).
如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,-1).