题目内容
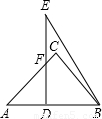
 将两块三角板如图放置,其中∠C=∠EDB=90°,∠A=45°,∠E=30°,AB=DE=
将两块三角板如图放置,其中∠C=∠EDB=90°,∠A=45°,∠E=30°,AB=DE= a,AC交ED于点F,求DB及AF的长.
a,AC交ED于点F,求DB及AF的长.
解:在Rt△EDB中,∠EDB=90°,∠E=30°,则 =
= ,
,
解得DB=a.
AD= a-a.
a-a.
在Rt△ADF中,∠ADF=90°,∠A=45°,则 =
= ,
,
即 =
= ,
,
解得AF= a-
a- a.
a.
分析:在Rt△EDB中,根据三角函数可求DB=a.从而得到AD= a-a;在Rt△ADF中根据三角函数可求AF的长.
a-a;在Rt△ADF中根据三角函数可求AF的长.
点评:考查了解直角三角形,此题要求我们综合利用解直角三角形,直角三角形的性质和三角函数的灵活运用来解答.
 =
= ,
,解得DB=a.
AD=
 a-a.
a-a.在Rt△ADF中,∠ADF=90°,∠A=45°,则
 =
= ,
,即
 =
= ,
,解得AF=
 a-
a- a.
a.分析:在Rt△EDB中,根据三角函数可求DB=a.从而得到AD=
 a-a;在Rt△ADF中根据三角函数可求AF的长.
a-a;在Rt△ADF中根据三角函数可求AF的长.点评:考查了解直角三角形,此题要求我们综合利用解直角三角形,直角三角形的性质和三角函数的灵活运用来解答.

练习册系列答案
相关题目
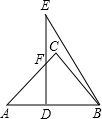 将两块三角板如图放置,其中∠C=∠EDB=90°,∠A=45°,∠E=30°,AB=DE=6,求重叠部分四边形DBCF的面积.
将两块三角板如图放置,其中∠C=∠EDB=90°,∠A=45°,∠E=30°,AB=DE=6,求重叠部分四边形DBCF的面积.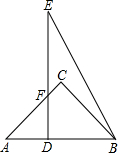 将两块三角板如图放置,其中∠C=∠EDB=90°,∠A=45°,∠E=30°,AB=DE=
将两块三角板如图放置,其中∠C=∠EDB=90°,∠A=45°,∠E=30°,AB=DE= 将两块三角板如图放置,其中∠C=∠EDB=90°,∠A=45°,∠E=30°,AB=DE=6,求重叠部分四边形DBCF的面积.
将两块三角板如图放置,其中∠C=∠EDB=90°,∠A=45°,∠E=30°,AB=DE=6,求重叠部分四边形DBCF的面积.