题目内容
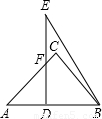
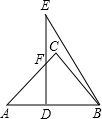 将两块三角板如图放置,其中∠C=∠EDB=90°,∠A=45°,∠E=30°,AB=DE=6,求重叠部分四边形DBCF的面积.
将两块三角板如图放置,其中∠C=∠EDB=90°,∠A=45°,∠E=30°,AB=DE=6,求重叠部分四边形DBCF的面积.
分析:观察可看出,所求四边形的面积等于等腰直角三角形的面积减去S△ADF,从而我们只要求出这两个三角形的面积即可,这要求我们综合利用解直角三角形,直角三角形的性质和三角函数的灵活运用来解答.
解答:解:在△EDB中,
∵∠EDB=90°,∠E=30°,DE=6,
∴DB=DE•tan30°=6×
=2
,
∴AD=AB-DB=6-2
.
又∵∠A=45°,∠AFD=45°,得FD=AD.
∴S△ADF=
AD2=
×(6-2
)2=24-12
.
在等腰直角三角形ABC中,斜边AB=6,
∴AC=BC=3
,
∴S△ABC=
AC2=9,
∴S四边形DBCF=S△ABC-S△ADF=9-(24-12
)=12
-15.
∵∠EDB=90°,∠E=30°,DE=6,
∴DB=DE•tan30°=6×
| ||
| 3 |
| 3 |
∴AD=AB-DB=6-2
| 3 |
又∵∠A=45°,∠AFD=45°,得FD=AD.
∴S△ADF=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
在等腰直角三角形ABC中,斜边AB=6,
∴AC=BC=3
| 2 |
∴S△ABC=
| 1 |
| 2 |
∴S四边形DBCF=S△ABC-S△ADF=9-(24-12
| 3 |
| 3 |
点评:此题要求我们综合利用解直角三角形,直角三角形的性质和三角函数的灵活运用来解答.

练习册系列答案
相关题目
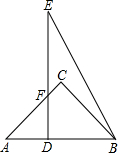 将两块三角板如图放置,其中∠C=∠EDB=90°,∠A=45°,∠E=30°,AB=DE=
将两块三角板如图放置,其中∠C=∠EDB=90°,∠A=45°,∠E=30°,AB=DE= 将两块三角板如图放置,其中∠C=∠EDB=90°,∠A=45°,∠E=30°,AB=DE=6,求重叠部分四边形DBCF的面积.
将两块三角板如图放置,其中∠C=∠EDB=90°,∠A=45°,∠E=30°,AB=DE=6,求重叠部分四边形DBCF的面积.