题目内容
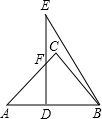（2013•宝山区一模）将两块三角板如图放置，其中∠C=∠EDB=90°，∠A=45°，∠E=30°，AB=DE=12，求重叠部分四边形DBCF的面积．分析：观察可看出，所求四边形的面积等于等腰直角三角形的面积减去S△ADF，从而我们只要求出这两个三角形的面积即可，这要求我们综合利用解直角三角形，直角三角形的性质和三角函数的灵活运用来解答．
解答：解：在△EDB中，∠EDB=90°，∠E=30°，DE=6，
∴DB=DE•tan30°=6×
=2
，
∴AD=AB-DB=6-2
，
又∵∠A=45°，∠AFD=45°，得FD=AD，
∴S△ADF=
AD2=
×（6-2
）2=24-12
，
在等腰直角三角形ABC中，斜边AB=6，
∴AC=BC=3
，
∴S△ABC=
AC2=9，
∴S四边形DBCF=S△ABC-S△ADF=9-（24-12
）=12
-15．
∴DB=DE•tan30°=6×
| ||
| 3 |
| 3 |
∴AD=AB-DB=6-2
| 3 |
又∵∠A=45°，∠AFD=45°，得FD=AD，
∴S△ADF=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
在等腰直角三角形ABC中，斜边AB=6，
∴AC=BC=3
| 2 |
∴S△ABC=
| 1 |
| 2 |
∴S四边形DBCF=S△ABC-S△ADF=9-（24-12
| 3 |
| 3 |
点评：此题考查了解直角三角形，涉及的知识有：勾股定理，等腰直角三角形的性质，锐角三角函数定义，熟练掌握直角三角形的性质是解本题的关键．
练习册系列答案
相关题目