题目内容
2.边心距为2的等边三角形边长是( )| A. | 4 | B. | 4$\sqrt{3}$ | C. | 2$\sqrt{3}$ | D. | 2 |
分析 根据题意画出图形,先根据等边三角形的性质得出∠OBD=30°,根据锐角三角函数的定义得出BD的长,由垂径定理即可得出结论.
解答 解:如图所示,
∵△ABC是等边三角形,边心距OD=2,
∴∠OBD=30°,
∴BD=$\frac{OD}{tan30°}$=2$\sqrt{3}$,
∵OD⊥BC,
∴BC=2BD=4$\sqrt{3}$.
故选:B.
点评 本题考查的是正多边形和圆、三角函数正三角形的性质;熟知正三角形的性质是解答此题的关键.

练习册系列答案
相关题目
14. 如图,△ABC中,AB=AC,BD=CE,CD=BF,若∠A=50°,则∠EDF=( )
如图,△ABC中,AB=AC,BD=CE,CD=BF,若∠A=50°,则∠EDF=( )
 如图,△ABC中,AB=AC,BD=CE,CD=BF,若∠A=50°,则∠EDF=( )
如图,△ABC中,AB=AC,BD=CE,CD=BF,若∠A=50°,则∠EDF=( )| A. | 80° | B. | 65° | C. | 50° | D. | 20° |
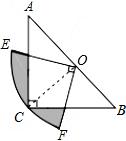 如图,在△ABC中,∠C=90°,AC=BC,斜边AB=2,O是AB的中点,以O为圆心,线段OC的长为半径画圆心角为90°的扇形OEF,$\widehat{EF}$经过点C,求:
如图,在△ABC中,∠C=90°,AC=BC,斜边AB=2,O是AB的中点,以O为圆心,线段OC的长为半径画圆心角为90°的扇形OEF,$\widehat{EF}$经过点C,求: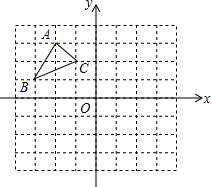 如图:在平面直角坐标系中,网格中每一个小正方形的边长为1个单位长度;已知△ABC.
如图:在平面直角坐标系中,网格中每一个小正方形的边长为1个单位长度;已知△ABC.