题目内容
S=1+
+
+…+
,求[S].
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| 20082 |
考点:取整计算
专题:计算题
分析:先把等式两边乘以2;由于(
-
)2≥0,则
+
≥
(a>0,b>0,当a与b相等时取等号),则2S>1+
+
+…+
+
,然后利用
=
-
进行计算得到2S>1+
+
,得到S>1.4546,再根据取整计算即可得到[S]=1.
| 1 |
| a |
| 1 |
| b |
| 1 |
| a2 |
| 1 |
| b2 |
| 2 |
| ab |
| 2 |
| 1×2 |
| 1 |
| 2×3 |
| 2 |
| 3×4 |
| 1 |
| 2007×2008 |
| 1 |
| 20082 |
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
| 2007 |
| 1004 |
| 1 |
| 20082 |
解答:解:根据
+
≥
得
2S=1+1+
+
+
+
+…+
+
,
∴2S>1+
+
+
+…+
+
,
∴2S>1+2×(1-
+
-
+
-
+…+
-
)+
,
∴2S>1+
+
,
∴S>1.4546,
∴[S]=1.
| 1 |
| a2 |
| 1 |
| b2 |
| 2 |
| ab |
2S=1+1+
| 1 |
| 22 |
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| 32 |
| 1 |
| 20082 |
| 1 |
| 20082 |
∴2S>1+
| 2 |
| 1×2 |
| 2 |
| 2×3 |
| 2 |
| 3×4 |
| 2 |
| 2007×2008 |
| 1 |
| 20082 |
∴2S>1+2×(1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2007 |
| 1 |
| 2008 |
| 1 |
| 20082 |
∴2S>1+
| 2007 |
| 1004 |
| 1 |
| 20082 |
∴S>1.4546,
∴[S]=1.
点评:本题考查了取整计算:[x]表示不大于x的最大整数.也考查了
+
≥
(a>0,b>0,当a与b相等时取等号)以及
=
-
.
| 1 |
| a2 |
| 1 |
| b2 |
| 2 |
| ab |
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |

练习册系列答案
相关题目
 如图,在?ABCD中,E是BC的中点,且∠AEC=∠DCE,则下列结论不正确的是( )
如图,在?ABCD中,E是BC的中点,且∠AEC=∠DCE,则下列结论不正确的是( )| A、AD=2BE | ||
B、BF=
| ||
| C、S△AFD=2S△AFB | ||
| D、S△AFD=2S△EFB |
 如图,梯形ABCD中,EF过对角线的交点O,且AD∥EF∥BC,AD=m,BC=n,则EF长为
如图,梯形ABCD中,EF过对角线的交点O,且AD∥EF∥BC,AD=m,BC=n,则EF长为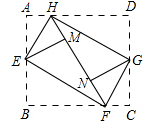 如图,将矩形ABCD的四个角向内折起,恰好拼成一个既无缝隙又无重叠的四边形EFGH,若EH=3,EF=4,那么线段AH:HD=
如图,将矩形ABCD的四个角向内折起,恰好拼成一个既无缝隙又无重叠的四边形EFGH,若EH=3,EF=4,那么线段AH:HD=