题目内容
1.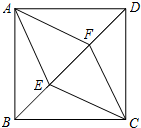 如图,在正方形ABCD中,点E、F在对角线BD上,且BE=EF=FD,连接AF、AE、CE、CF,请你判断四边形AECF的形状,并证明你的结论.
如图,在正方形ABCD中,点E、F在对角线BD上,且BE=EF=FD,连接AF、AE、CE、CF,请你判断四边形AECF的形状,并证明你的结论.
分析 根据正方形的性质,即可判定△ABE≌△ADF,得出AE=AF,CE=CF,判定△ADF≌△CDF,即可得出AF=CF,根据AE=AF=CF=CE,可得四边形AECF是菱形.
解答 解:四边形AECF是菱形.
∵在正方形ABCD中,AB=AD,
∴∠ABE=∠ADF,
又∵BE=DF,
∴△ABE≌△ADF,
∴AE=AF,
同理可得,CE=CF,
∵在正方形ABCD中,CD=AD,∠CDE=∠ADF,DF=DF,
∴△ADF≌△CDF,
∴AF=CF,
∴AE=AF=CF=CE,
∴四边形AECF是菱形.
点评 本题主要考查了正方形的性质,全等三角形的判定与性质以及菱形的判定,解题时注意:四条边相等的四边形是菱形.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
11.小派同学想给数学老师送张生日贺卡,但他只知道老师的生日在10月,那么他一次猜中老师生日的概率是( )
| A. | $\frac{1}{28}$ | B. | $\frac{1}{29}$ | C. | $\frac{1}{30}$ | D. | $\frac{1}{31}$ |
9.在长春市2016年地铁建设中,某工程队挖掘土方为632000立方米,632000这个数用科学记数法表示为( )
| A. | 63.2×104 | B. | 6.32×105 | C. | 0.632×106 | D. | 6.32×106 |
11.下列四个角中,∠1、∠2是同位角的有( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
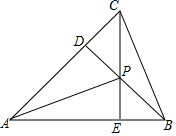 如图,△ABC的两条高BD、CE相交于点P,且PD=PE.求证:AC=AB.
如图,△ABC的两条高BD、CE相交于点P,且PD=PE.求证:AC=AB. 如图,在四边形ABCD中,AB=CD,BC=AD,若∠A=130°,则∠C=130度.
如图,在四边形ABCD中,AB=CD,BC=AD,若∠A=130°,则∠C=130度.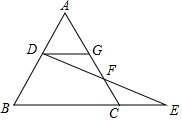 已知:如图,点D在等边△ABC的边AB上,作DG∥BC,交AC于点G,点F在边AC上,连接DF并延长,交BC的延长线于点E,FE=FD.求证:AD=CE.
已知:如图,点D在等边△ABC的边AB上,作DG∥BC,交AC于点G,点F在边AC上,连接DF并延长,交BC的延长线于点E,FE=FD.求证:AD=CE.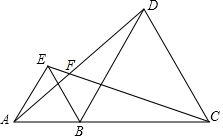 如图所示,点A,B,C在同一条直线上,△ABE和△BCD都是等边三角形(等边三角形每个内角都是60°).
如图所示,点A,B,C在同一条直线上,△ABE和△BCD都是等边三角形(等边三角形每个内角都是60°).