题目内容
11.计算:(1)$\frac{{x}^{2}-6x+9}{1+4x+4{x}^{2}}$÷$\frac{12-4x}{2x+1}$
(2)$\frac{b}{a-b}$+$\frac{a}{a+b}$+$\frac{2ab}{{a}^{2}-{b}^{2}}$.
分析 (1)原式利用除法法则变形,约分即可得到结果;
(2)原式通分并利用同分母分式的加法法则计算即可得到结果.
解答 解:(1)原式=$\frac{(x-3)^{2}}{(2x+1)^{2}}$•$\frac{2x+1}{-4(x-3)}$=-$\frac{x-3}{8x+4}$;
(2)原式=$\frac{ab+{b}^{2}+{a}^{2}-ab+2ab}{(a+b)(a-b)}$=$\frac{(a+b)^{2}}{(a+b)(a-b)}$=$\frac{a+b}{a-b}$.
点评 此题考查了分式的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
19.在$\sqrt{15}$,$\sqrt{\frac{1}{6}}$,$\sqrt{1\frac{1}{2}}$,$\sqrt{40}$,$\sqrt{0.2}$中最简二次根式的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
6.今年我市有近2万名考生参加中考,为了解这些考生的数学成绩,从中抽取1000名考生的数学成绩进行统计分析,以下说法正确的是( )
| A. | 这1000名考生是总体的一个样本 | B. | 近2万名考生是总体 | ||
| C. | 每位考生的数学成绩是个体 | D. | 1000名学生是样本容量 |
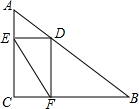 如图,Rt△ABC中,∠ACB=90°,AC=3,BC=4,D是AB上一动点,过点D作DE⊥AC于点E,DF⊥BC于点F,连接EF,则线段EF的最小值是( )
如图,Rt△ABC中,∠ACB=90°,AC=3,BC=4,D是AB上一动点,过点D作DE⊥AC于点E,DF⊥BC于点F,连接EF,则线段EF的最小值是( )
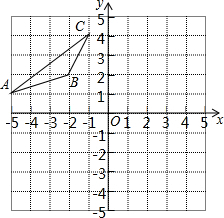 如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-5,1),B(-2,2),C(-1,4),请按下列要求画图:
如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-5,1),B(-2,2),C(-1,4),请按下列要求画图: