题目内容
 如图,∠B=∠C,B,A,D三点在同一直线上,∠DAC=∠B+∠C,AE是∠DAC的平分线,求证:AE∥BC.
如图,∠B=∠C,B,A,D三点在同一直线上,∠DAC=∠B+∠C,AE是∠DAC的平分线,求证:AE∥BC.考点:平行线的判定
专题:证明题
分析:先根据∠B=∠C,∠DAC=∠B+∠C得出∠DAC=2∠B,再由AE是∠DAC的平分线可知∠1=∠2,∠DAC=2∠1,故∠1=∠B,由此可得出结论.
解答:证明:∵∠B=∠C,∠DAC=∠B+∠C,
∴∠DAC=2∠B.
∵AE是∠DAC的平分线,
∴∠1=∠2,∠DAC=2∠1,
∴∠1=∠B,
∴AE∥BC.
∴∠DAC=2∠B.
∵AE是∠DAC的平分线,
∴∠1=∠2,∠DAC=2∠1,
∴∠1=∠B,
∴AE∥BC.
点评:本题考查的是平行线的判定定理,用到的知识点为:同位角相等,两直线平行.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
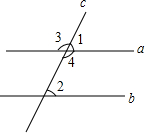 如图,已知∠3=115°,∠2=65°,问直线a,b平行?
如图,已知∠3=115°,∠2=65°,问直线a,b平行? 已知:如图,直线a,b,c被直线d所截,∠2=∠3,∠1+∠3=180°.找出图中的平行线,并给出证明.
已知:如图,直线a,b,c被直线d所截,∠2=∠3,∠1+∠3=180°.找出图中的平行线,并给出证明.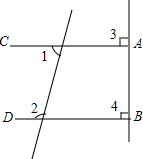 如图,已知CA⊥BA于A,DB⊥AB于B,∠1与∠2有什么关系?说明理由.
如图,已知CA⊥BA于A,DB⊥AB于B,∠1与∠2有什么关系?说明理由.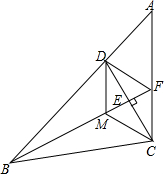 如图,在△ABC中,D是AB上一点,且BD=BC,BF⊥CD于点E,交AC于点F,M为线段BE上任意一点,请探究,当ME与EF满足什么数量关系时四边DMCF是菱形?
如图,在△ABC中,D是AB上一点,且BD=BC,BF⊥CD于点E,交AC于点F,M为线段BE上任意一点,请探究,当ME与EF满足什么数量关系时四边DMCF是菱形?