题目内容
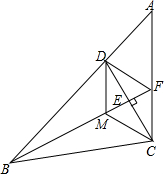如图，在△ABC中，D是AB上一点，且BD=BC，BF⊥CD于点E，交AC于点F，M为线段BE上任意一点，请探究，当ME与EF满足什么数量关系时四边DMCF是菱形？考点：菱形的判定
专题：
分析：首先得到四边形DMCF是平行四边形，然后根据对角线垂直平分的四边形是菱形进行证明即可．
解答：答：当ME=EF时，四边形DMEF为菱形；
证明：∵BD=BC BF⊥CD于点，
∴DE=CE（等腰三角形三线合一），
∵DE=CE，ME=EF，
∴四边形DMEF为平行四边形，
BF⊥CD，ME=EF，
∴CD垂直平分MF，
∴DM=DF（垂直平分线性质），
∵平行四边形DMEF中DM=DF，
∴四边形DMEF为菱形（邻边相等的平行四边形是菱形）．
证明：∵BD=BC BF⊥CD于点，
∴DE=CE（等腰三角形三线合一），
∵DE=CE，ME=EF，
∴四边形DMEF为平行四边形，
BF⊥CD，ME=EF，
∴CD垂直平分MF，
∴DM=DF（垂直平分线性质），
∵平行四边形DMEF中DM=DF，
∴四边形DMEF为菱形（邻边相等的平行四边形是菱形）．
点评：本题考查了菱形的判定，牢记菱形的判定定理是解得本题的关键，难度不大．
练习册系列答案
相关题目
如图，∠B=∠C，B，A，D三点在同一直线上，∠DAC=∠B+∠C，AE是∠DAC的平分线，求证：AE∥BC．
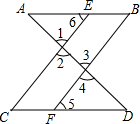如图，已知∠1=∠4，∠B=∠C，判断∠A与∠D的大小关系，并说明理由．小明同学给出了如下解答．
如图，一楼高20m，一只鸽子从地面的A处沿倾斜角为30°的方向直飞楼顶的B处，则鸽子飞行的路程是
如图，在三角形ABC中，点D，E，F分别在AB，AC，BC上，DE∥BC，已知∠A=60°，∠DFB=75°，∠ADE=45°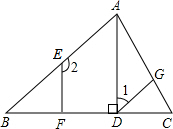
如图，AD是△ABC的高，点E、G分别在AB、AC上，EF⊥BC，垂足为F，∠1+∠2=180°．∠CGD与∠BAC相等吗？为什么？