题目内容
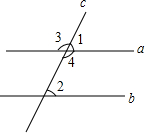 如图,已知∠3=115°,∠2=65°,问直线a,b平行?
如图,已知∠3=115°,∠2=65°,问直线a,b平行?解:∵∠3和∠4是对顶角,
∴∠4=∠3=115°(
∵∠2=65°
∴∠2+∠4=
∴a∥b(
考点:平行线的判定
专题:推理填空题
分析:由条件可求得∠4,可得出∠2+∠4=180°,可判定a∥b,依次填空即可.
解答:解:∵∠3和∠4是对顶角,
∴∠4=∠3=115°( 对顶角相等),
∵∠2=65°
∴∠2+∠4=∠2+∠3=180°,
∴a∥b( 同旁内角互补,两直线平行),
故答案为:对顶角;∠2;∠3;180°.
∴∠4=∠3=115°( 对顶角相等),
∵∠2=65°
∴∠2+∠4=∠2+∠3=180°,
∴a∥b( 同旁内角互补,两直线平行),
故答案为:对顶角;∠2;∠3;180°.
点评:本题主要考查平行线的判定,掌握平行线的判定和性质是解题的关键,即①同位角相等?两直线平行,②内错角相等?两直线平行,③同旁内角互补?两直线平行,④a∥b,b∥c?a∥c.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
相关题目
 如图,下列条件能判定a∥b的是( )
如图,下列条件能判定a∥b的是( )| A、∠1=∠2 |
| B、∠1+∠2=180° |
| C、∠2+∠3=180° |
| D、∠3=∠4 |
 如图,∠ABC=∠BCD,∠1=∠2,求证:BE∥CF.
如图,∠ABC=∠BCD,∠1=∠2,求证:BE∥CF. 如图,在?ABCD中,平行于AB的直线交BC于点P,交AD于点Q,M为AP、BQ的交点,N为DP、CQ的交点,猜想MN与AD的关系并说明理由.
如图,在?ABCD中,平行于AB的直线交BC于点P,交AD于点Q,M为AP、BQ的交点,N为DP、CQ的交点,猜想MN与AD的关系并说明理由. 如图,∠B=∠C,B,A,D三点在同一直线上,∠DAC=∠B+∠C,AE是∠DAC的平分线,求证:AE∥BC.
如图,∠B=∠C,B,A,D三点在同一直线上,∠DAC=∠B+∠C,AE是∠DAC的平分线,求证:AE∥BC.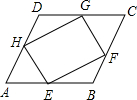 如图,已知E,F,G,H分别是?ABCD的边AB,BC,CD,DA上的点,且AE=CG,BF=DH.求证:四边形EFGH是平行四边形.
如图,已知E,F,G,H分别是?ABCD的边AB,BC,CD,DA上的点,且AE=CG,BF=DH.求证:四边形EFGH是平行四边形.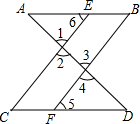 如图,已知∠1=∠4,∠B=∠C,判断∠A与∠D的大小关系,并说明理由.小明同学给出了如下解答.
如图,已知∠1=∠4,∠B=∠C,判断∠A与∠D的大小关系,并说明理由.小明同学给出了如下解答.