题目内容
任意△ABC中，∠B=2∠C，∠A、∠B、∠C对应边为a、b、c．求证：b2=c（a+c）．
考点：相似三角形的判定与性质
专题：证明题
分析：如图，作辅助线，证明△ADB∽△DCA，进而证明
=
，化为等积式问题即可解决．
| AD |
| DC |
| AB |
| AC |
解答：
证明：如图，延长CB到点D，使BD=BA；
则∠D=∠DAB=α；∠B=∠D+∠DAB=2α；
∵∠B=2∠C，
∴2∠C=2α，∠D=∠C=α，AD=AC=b；
∵∠D=∠DAB=∠C，
∴△ADB∽△DCA，
∴
=
，而AD=b，AB=c，DC=a+c，AC=b，
∴b2=c（a+c）．
证明：如图，延长CB到点D，使BD=BA；则∠D=∠DAB=α；∠B=∠D+∠DAB=2α；
∵∠B=2∠C，
∴2∠C=2α，∠D=∠C=α，AD=AC=b；
∵∠D=∠DAB=∠C，
∴△ADB∽△DCA，
∴
| AD |
| DC |
| AB |
| AC |
∴b2=c（a+c）．
点评：该题主要考查了相似三角形的判定及其性质的应用问题；解题的关键是作辅助线，构造相似三角形；灵活运用有关定理来分析、判断、推理或解答是解题的关键．
练习册系列答案
相关题目
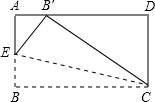如图，一块矩形纸片的宽CD为2cm，点E在AB上，如果沿图中的EC对折，B点刚好落在AD上，此时∠BCE=15°，则BC的长为
如图，直线EF，CD相交于点O，∠AOB=90°，且OD平分∠AOF，∠BOE=2∠AOE，求∠EOD的度数．
如图，圆内接四边形ABCD中，AC、BD相交于E，且AE=CE，求证：