题目内容
11.已知抛物线y=a(x-h)2+k经过点(0,2)(1,5),有下列结论:①若a=-1,则h=2,k=6;②若k≥5,则a<0;③若a<0,则h>$\frac{1}{2}$.
其中,正确的个数是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 把两点代入可确定出a、h、k三者之间的关系,再分别判断三个结合即可.
解答 解:∵抛物线y=a(x-h)2+k经过点(0,2)(1,5),
∴把两点坐标代入可得$\left\{\begin{array}{l}{2=a{h}^{2}+k}\\{5=a(1-h)^{2}+k}\end{array}\right.$整理得:a-2ah=3
当a=-1时,则1+2h=5,解得h=2,k=6,
故①正确;
当k≥5时,则2-ah2≥5,
∴ah2≤-3,
∴a<0,
故②正确;
∵a-2ah=3,
∴a(1-2h)=3,
∴当a<0时,1-2h<0,解得h>$\frac{1}{2}$,
故③正确;
综上可知正确的结论有3个,
故选D.
点评 本题主要考查抛物线的性质,根据条件得到a、h、k之间的关系式是解题的关键.

练习册系列答案
相关题目
6.下列计算正确的有几个( )
①$\frac{a+1}{a-1}=-1$;②$\frac{(a-b)^{2}}{(b-a)^{2}}=-1$;③$\frac{6-2x}{-x+3}=2$;④$\frac{{x}^{2}+{y}^{2}}{x+y}=x+y$.
①$\frac{a+1}{a-1}=-1$;②$\frac{(a-b)^{2}}{(b-a)^{2}}=-1$;③$\frac{6-2x}{-x+3}=2$;④$\frac{{x}^{2}+{y}^{2}}{x+y}=x+y$.
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
1.下列等式正确的是( )
| A. | 3-2=-9 | B. | -0.000000137=-1.37×107 | ||
| C. | (a2)-3=$\frac{1}{{a}^{6}}$ | D. | -$\frac{x-1}{x-y}$=$\frac{x+1}{x-y}$ |
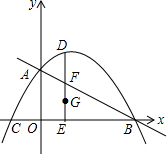 如图,抛物线y=ax2+bx+2与坐标轴交于A、B、C三点,其中B(4,0)、C(-2,0),连接AB、AC,在第一象限内的抛物线上有一动点D,过D作DE⊥x轴,垂足为E,交AB于点F.
如图,抛物线y=ax2+bx+2与坐标轴交于A、B、C三点,其中B(4,0)、C(-2,0),连接AB、AC,在第一象限内的抛物线上有一动点D,过D作DE⊥x轴,垂足为E,交AB于点F.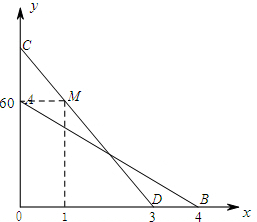 如图,线段AB、CD分别是一辆轿车和一辆客车在行驶过程中油箱内的剩余油量y1(升)、y2(升)关于行驶时间x(小时)的函数图象.
如图,线段AB、CD分别是一辆轿车和一辆客车在行驶过程中油箱内的剩余油量y1(升)、y2(升)关于行驶时间x(小时)的函数图象.