题目内容
6. 如图,在平面直角坐标系中,⊙P的半径为5,圆心P坐标是(5,a)(a>5),函数y=x的图象被⊙P截得的弦AB的长为4$\sqrt{6}$,则a的值是5+$\sqrt{2}$.
如图,在平面直角坐标系中,⊙P的半径为5,圆心P坐标是(5,a)(a>5),函数y=x的图象被⊙P截得的弦AB的长为4$\sqrt{6}$,则a的值是5+$\sqrt{2}$.
分析 作PC⊥x轴于C,交AB于D,作PE⊥AB于E,连结PB,由于OC=5,PC=a,易得D点坐标为(5,5),则△OCD为等腰直角三角形,△PED也为等腰直角三角形.由PE⊥AB,根据垂径定理得AE=BE=$\frac{1}{2}$AB=2$\sqrt{6}$,在Rt△PBE中,利用勾股定理可计算出PE=1,则PD=$\sqrt{2}$PE=$\sqrt{2}$,所以a=5+$\sqrt{2}$.
解答 解:作PC⊥x轴于C,交AB于D,作PE⊥AB于E,连结PB,如图,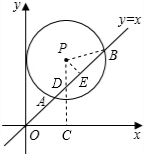 ∵⊙P的圆心坐标是(5,a),
∵⊙P的圆心坐标是(5,a),
∴OC=5,PC=a,
把x=5代入y=x得y=5,
∴D点坐标为(5,5),
∴CD=5,
∴△OCD为等腰直角三角形,
∴△PED也为等腰直角三角形,
∵PE⊥AB,
∴AE=BE=$\frac{1}{2}$AB=$\frac{1}{2}$×4$\sqrt{6}$=2$\sqrt{6}$,
在Rt△PBE中,PB=5,
∴PE=$\sqrt{{5}^{2}-(2\sqrt{6})^{2}}$=1,
∴PD=$\sqrt{2}$PE=$\sqrt{2}$,
∴a=5+$\sqrt{2}$.
故答案为:5+$\sqrt{2}$.
点评 本题考查了圆的综合题,垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了勾股定理和等腰直角三角形的性质.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.在下面的图形中是正方体的展开图的是( )
| A. |  | B. |  | C. |  | D. |  |
1.如果零上2℃记作+2℃,那么零下3℃记作( )
| A. | +2℃ | B. | -2℃ | C. | +3℃ | D. | -3℃ |
16.若一元二次方程ax2+bx+c=0没有实数根,则二次函数y=ax2+bx+c的图象与x轴的交点有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 无数个 |
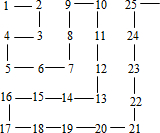 将正整数从1开始,按如图所表示的规律排列.规定图中第m行、第n列的位置记作(m,n),如正整数8的位置是(2,3),则正整数137的位置记作(12,8).
将正整数从1开始,按如图所表示的规律排列.规定图中第m行、第n列的位置记作(m,n),如正整数8的位置是(2,3),则正整数137的位置记作(12,8).