题目内容
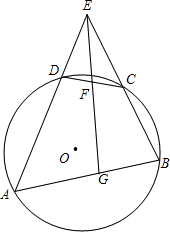 如图,已知⊙O是四边形ABCD的外接圆,直线AD,BC相交于点E,F是弦CD的中点,直线EF交弦AB于点G,求证:
如图,已知⊙O是四边形ABCD的外接圆,直线AD,BC相交于点E,F是弦CD的中点,直线EF交弦AB于点G,求证:
(1)ED•EA=EC•EB;
(2)AG:GB=AE2:BE2.
证明:
(1)∵四边形ABCD是⊙O的内接四边形
∴∠DCE=∠A,∠EDC=∠B
∴△EDC∽△EAB
∴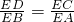
故ED•EA=EC•EB;
(2)证明:∵△DEF的边DF和△CEF的边CF上的高相等,
∵CF=DF,
∴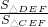 =1,
=1,
由正弦定理得: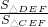 =
=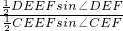 =
=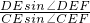 =1
=1
∵△EDC∽△EAB
∴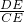 =
= ,
,
∴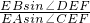 =1,
=1,
∴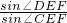 =
= ,
,
∵△AEG边AG和△BEG边CG上的高相等,
∴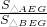 =
= =
=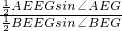 =
= •
•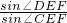 =
= ×
× ,
,
即 =
= .
.
分析:(1)由四边形ABCD是⊙O的内接四边形,据此性质证△EDC∽△EAB,从而得证;
(2)根据三角形面积公式和CF=DF求出,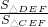 =1,由正弦定理推出
=1,由正弦定理推出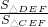 =1根据△EDC∽△EAB求出
=1根据△EDC∽△EAB求出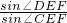 =
= ,根据三角形面积公式求出
,根据三角形面积公式求出 =
= =
= •
•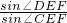 ,代入求出即可.
,代入求出即可.
点评:此题考查的知识点是相似三角形的判定与性质,解答此题的关键是运用好圆内接四边形的性质和三角形的面积公式.
(1)∵四边形ABCD是⊙O的内接四边形
∴∠DCE=∠A,∠EDC=∠B
∴△EDC∽△EAB
∴
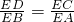
故ED•EA=EC•EB;
(2)证明:∵△DEF的边DF和△CEF的边CF上的高相等,
∵CF=DF,
∴
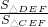 =1,
=1,由正弦定理得:
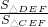 =
=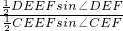 =
=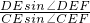 =1
=1∵△EDC∽△EAB
∴
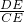 =
= ,
,∴
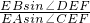 =1,
=1,∴
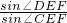 =
= ,
,∵△AEG边AG和△BEG边CG上的高相等,
∴
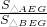 =
= =
=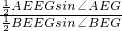 =
= •
•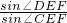 =
= ×
× ,
,即
 =
= .
.分析:(1)由四边形ABCD是⊙O的内接四边形,据此性质证△EDC∽△EAB,从而得证;
(2)根据三角形面积公式和CF=DF求出,
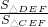 =1,由正弦定理推出
=1,由正弦定理推出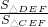 =1根据△EDC∽△EAB求出
=1根据△EDC∽△EAB求出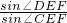 =
= ,根据三角形面积公式求出
,根据三角形面积公式求出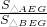 =
= =
= •
• ,代入求出即可.
,代入求出即可.点评:此题考查的知识点是相似三角形的判定与性质,解答此题的关键是运用好圆内接四边形的性质和三角形的面积公式.

练习册系列答案
相关题目
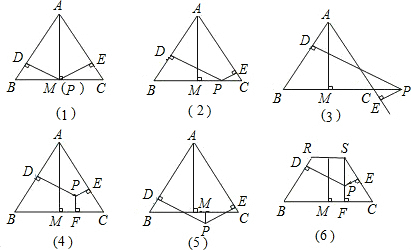
 如图:已知点M、N、P、Q分别为菱形ABCD四边上的中点,下列说法正确的是( )
如图:已知点M、N、P、Q分别为菱形ABCD四边上的中点,下列说法正确的是( )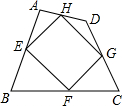 如图,已知E、F、G、H是四边形ABCD四边的中点,则四边形EFGH的形状为
如图,已知E、F、G、H是四边形ABCD四边的中点,则四边形EFGH的形状为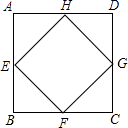 如图,已知正方形ABCD的面积是64cm2,依次连接正方形的四边中点E、F、G、H得到小正方形EFGH.求这个小正方形EFGH的边长(结果保留两个有效数字).
如图,已知正方形ABCD的面积是64cm2,依次连接正方形的四边中点E、F、G、H得到小正方形EFGH.求这个小正方形EFGH的边长(结果保留两个有效数字).