题目内容
 如图:已知点M、N、P、Q分别为菱形ABCD四边上的中点,下列说法正确的是( )
如图:已知点M、N、P、Q分别为菱形ABCD四边上的中点,下列说法正确的是( )分析:根据中点四边形的判定得到四边形MNPQ为矩形,然后利用矩形和菱形的性质作出判断即可.
解答:解:A、顺次连接菱形四边中点得到的四边形是矩形,故本选项错误;
B、矩形不可能和菱形位似,故本选项错误;
C、利用中位线的性质可知矩形的周长等于对角线的和,而菱形的周长不等于其两条对角线的和,故本选项错误;
D、利用菱形和矩形的面积计算方法可知:设对角线长分别为a、b,菱形的面积为
ab,矩形的面积等于
a×
b=
ab,所以两图形的比为1:2,故本选项正确.
故选D.
B、矩形不可能和菱形位似,故本选项错误;
C、利用中位线的性质可知矩形的周长等于对角线的和,而菱形的周长不等于其两条对角线的和,故本选项错误;
D、利用菱形和矩形的面积计算方法可知:设对角线长分别为a、b,菱形的面积为
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
故选D.
点评:本题考查了位似变换、三角形的中位线定理及菱形的判定及性质,解决本题的关键是正确的证明中点四边形.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,已知点A、B、C、D均在已知圆上,AD∥BC,AC平分∠BCD,∠ADC=120°,四边形ABCD的周长为10cm.图中阴影部分的面积为( )
如图,已知点A、B、C、D均在已知圆上,AD∥BC,AC平分∠BCD,∠ADC=120°,四边形ABCD的周长为10cm.图中阴影部分的面积为( )A、
| ||||
B、
| ||||
C、2
| ||||
D、4
|
 16、如图,已知点D是∠ABC的平分线上一点,点P在BD上,PA⊥AB,PC⊥BC,垂足分别为A,C、下列结论错误的是( )
16、如图,已知点D是∠ABC的平分线上一点,点P在BD上,PA⊥AB,PC⊥BC,垂足分别为A,C、下列结论错误的是( )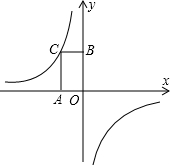 如图,已知点C为反比例函数y=-
如图,已知点C为反比例函数y=- 如图,已知点D为△ABC中AC边上一点,且AD:DC=3;4,设
如图,已知点D为△ABC中AC边上一点,且AD:DC=3;4,设 如图,已知点C为AB上一点,AC=12cm,CB=
如图,已知点C为AB上一点,AC=12cm,CB=