Question

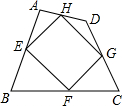如图，已知E、F、G、H是四边形ABCD四边的中点，则四边形EFGH的形状为

平行四边形

；如四边形ABCD的对角线AC与BD的和为40，则四边形EFGH的周长为

40

．

Answer 1

分析：利用三角形的中位线定理求出四边形EFGH的两组对边相等，即可证得四边形EFGH是平行四边形，继而即可求得EFGH的周长．

解答：解：连接AC、BD，

∵E、F、G、H分别为四边形ABCD四边的中点，
∴EH=

1

2

BD，FG=

1

2

BD，HG=

1

2

AC，EF=

1

2

AC，
∴EH=FG，EF=HG，
∴四边形EFGH是平行四边形．
∴四边形EFGH的周长=EH+HG+FG+EF=

1

2

×2×AC+

1

2

×2×BD=AC+BD=40．
故答案为：平行四边形；40．

点评：本题考查了平行四边形的判定及三角形中位线定理，三角形中位线性质应用比较广泛，尤其是在三角形、四边形方面起着非常重要作用，本题解题的关键是将四边形分为四个三角形，然后利用中位线定理解答．