题目内容
15.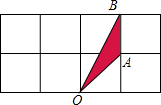 如图为正方形网格,每个小正方形的边长均为1,将△OAB绕点O逆时针旋转90°.
如图为正方形网格,每个小正方形的边长均为1,将△OAB绕点O逆时针旋转90°.(1)请画出△OAB旋转后的图形△OA′B′;
(2)求出点A所经过的路径的长.
分析 (1)利用网格特点和旋转的性质画出A点和B点的对应点A′、B′,从而得到△OA′B′;
(2)由于点A所经过的路径是以点O为圆心,$\sqrt{2}$为半径,圆心角为90°的弧,于是可根据弧长公式求解.
解答 解:(1)如图,△OA′B′为所作;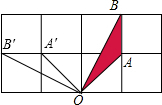
(2)∵△OAB绕点O逆时针旋转90°,
∴∠AOA′=90°,
而OA=$\sqrt{2}$,
∴点A所经过的路径的长=$\frac{90•π•\sqrt{2}}{180}$=$\frac{\sqrt{2}}{2}$π.
点评 本题考查了作图-旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.也考查了弧长的计算.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
3.抛物线y=3(x-3)2+1的顶点坐标是( )
| A. | (3,1) | B. | (3,-1) | C. | (-3,1) | D. | (-3,-1) |
7.下列说法正确的是( )
| A. | 长度相等的弧是等弧 | |
| B. | 圆既是轴对称图形,又是中心对称图形 | |
| C. | 弧是半圆 | |
| D. | 三点确定一个圆 |